⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-05-funkcja-liniowa-pp-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-10814 ⋅ Poprawnie: 266/526 [50%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
» Na rysunku przedstawiono wykres prostej:
Prosta symetryczna do tej prostej względem osi Ox
określona jest równaniem ax+by=4.
Podaj współczynniki a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10817 ⋅ Poprawnie: 126/215 [58%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Dane są funkcje f(x)=-2x-3 oraz
g(x)=f(x-1)+4. Zapisz wzór funkcji g
w postaci g(x)=ax+b.
Podaj współczynniki a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10808 ⋅ Poprawnie: 197/380 [51%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji
y=f(x):
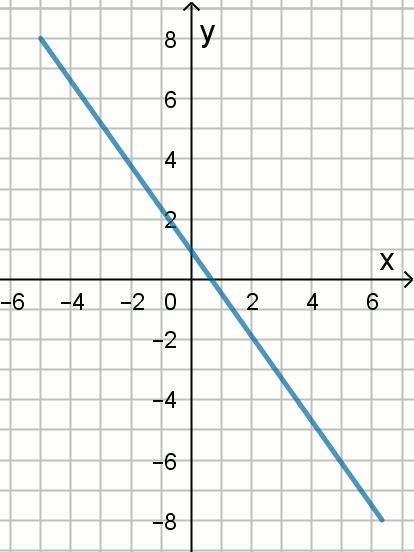
Wskaż wzór funkcji, której wykres jest symetryczny do tego wykresu względem osi Ox:
Odpowiedzi:
| A. y=\frac{1}{\sqrt{3}}x+1 | B. y=-\frac{\sqrt{3}}{3}x+1 |
| C. y=\sqrt{3}x-1 | D. y=\sqrt{3}x+1 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10793 ⋅ Poprawnie: 482/633 [76%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Liczba ......... jest miejscem zerowym funkcji określonej wzorem
f(x)=\frac{1}{10}x+\frac{1}{10}.
Podaj brakującą liczbę.
Odpowiedź:
| \frac{m}{n}= | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10941 ⋅ Poprawnie: 163/214 [76%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Dana jest funkcja liniowa określona wzorem
g(x)=(\sqrt{15}+\sqrt{8})x-7
.
Miejscem zerowym funkcji g jest liczba
\frac{\sqrt{8}-\sqrt{15}}{......}.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 6. 1 pkt ⋅ Numer: pp-11503 ⋅ Poprawnie: 661/948 [69%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Funkcje liniowe określone wzorami f(x)=\frac{1}{8}x-5 oraz
g(x)=mx+2 mają wspólne miejsce zerowe.
Wyznacz m.
Odpowiedź:
| m= | |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10899 ⋅ Poprawnie: 81/113 [71%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Punkty o współrzędnych (600,600) oraz
(900,-500) należą do wykresu funkcji liniowej
y=mx+n.
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : z treści wynika, że n=0 | T/N : z treści wynika, że m > 0 |
| T/N : z treści wynika, że n \lessdot 0 |
| Zadanie 8. 1 pkt ⋅ Numer: pp-10881 ⋅ Poprawnie: 190/246 [77%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Wyznacz zbiór tych wszystkich wartości parametru m, dla których
funkcja liniowa określona wzorem f(x)=\left(m^2-\frac{1}{36}\right)x+1296
jest malejąca. Rozwiązanie zapisz w postaci sumy przedziałów.
Podaj najmniejszy i największy z końców liczbowych tych przedziałów.
Odpowiedzi:
| min | = | (dwie liczby całkowite) | |
| max | = | (dwie liczby całkowite) | |
| Zadanie 9. 1 pkt ⋅ Numer: pp-10892 ⋅ Poprawnie: 243/364 [66%] | Rozwiąż |
Podpunkt 9.1 (0.8 pkt)
Funkcja liniowa określona wzorem f(x)=8+6x-12mx jest malejąca, wtedy i tylko wtedy,
gdy liczba m należy do pewnego przedziału.
Podaj koniec tego przedziału, który jest liczbą wymierną niecałkowitą.
Odpowiedź:
| \frac{k}{n}= | |
Podpunkt 9.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. -\infty | B. 4 |
| C. -3 | D. -2 |
| E. +\infty | F. 0 |
| Zadanie 10. 1 pkt ⋅ Numer: pp-10913 ⋅ Poprawnie: 76/139 [54%] | Rozwiąż |
Podpunkt 10.1 (0.8 pkt)
Wyznacz przedział tych wszystkich wartości m, dla których funkcja liniowa f(x)=\left(-\frac{10}{3}m+3\right)x-m
jest rosnąca.
Podaj koniec tego przedziału, który jest liczbą wymierną niecałkowitą.
Odpowiedź:
| \frac{k}{n}= | |
Podpunkt 10.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. -\infty | B. +\infty |
| C. 10 | D. 9 |
| E. -9 | F. -3 |
| Zadanie 11. 1 pkt ⋅ Numer: pp-10898 ⋅ Poprawnie: 71/119 [59%] | Rozwiąż |
Podpunkt 11.1 (1 pkt)
Wykres funkcji liniowej y=2^{27}x-2^{26} przechodzi przez
ćwiartki układu współrzędnych:
Odpowiedzi:
| A. II, III, IV | B. I, III i IV |
| C. I, II i IV | D. I, II i III |
| Zadanie 12. 1 pkt ⋅ Numer: pp-10878 ⋅ Poprawnie: 216/407 [53%] | Rozwiąż |
Podpunkt 12.1 (0.8 pkt)
Funkcja określona wzorem
f(x)=\left(\frac{1}{10}-\frac{\sqrt{3}}{7}m\right)x+2 jest rosnąca,
gdy parametr m należy do pewnego przedziału.
Podaj koniec tego przedziału, który jest liczbą niewymierną.
Odpowiedź:
| \frac{k\sqrt{n}}{p}= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 12.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. -\frac{7}{90} | B. -\frac{7}{20} |
| C. -\infty | D. \frac{7}{90} |
| E. -\frac{7}{60} | F. \frac{7}{15} |
| Zadanie 13. 1 pkt ⋅ Numer: pp-10800 ⋅ Poprawnie: 47/76 [61%] | Rozwiąż |
Podpunkt 13.1 (0.8 pkt)
Nierówności \left(6+\sqrt{37}\right)\left(\sqrt{37}-6\right)x > 2x-4
oraz (6-3x)^2+3x\leqslant (3x+6)^2-5x+4 są spełnione
przez każdą liczbę z pewnego przedziału.
Podaj lewy koniec tego przedziału.
Odpowiedź:
| Wpisz odpowiedź: | |
Podpunkt 13.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. 4 | B. -\infty |
| C. +\infty | D. -2 |
| Zadanie 14. 1 pkt ⋅ Numer: pp-10938 ⋅ Poprawnie: 121/181 [66%] | Rozwiąż |
Podpunkt 14.1 (1 pkt)
Punkt A=(m^2+1,-3) należy do wykresu funkcji liniowej
określonej wzorem g(x)=17-2x:
Odpowiedzi:
| A. tylko dla m=3 | B. dla m\in\{-3,3\} |
| C. tylko dla m=-3 | D. dla m\in\mathbb{R} |
| E. dla m\in\emptyset | F. tylko dla m=-6 |
| Zadanie 15. 1 pkt ⋅ Numer: pp-10737 ⋅ Poprawnie: 117/206 [56%] | Rozwiąż |
Podpunkt 15.1 (0.8 pkt)
« Dana jest funkcja określona wzorem f(x)=\frac{7}{9}x+1.
Funkcja ta wartości ujemne przyjmuje dla argumentów z pewnego przedziału.
Podaj ten koniec tego przedziału, który jest liczbą wymierną niecałkowitą.
Odpowiedź:
| Wpisz odpowiedź: | |
Podpunkt 15.2 (0.2 pkt)
Drugim końcem tego przedziału jest:
Odpowiedzi:
| A. 9 | B. +\infty |
| C. -9 | D. -\infty |
| E. -7 | F. 7 |