⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-06-ukl-row-lin-pp-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-10872 ⋅ Poprawnie: 377/496 [76%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Którą parę prostych pokazano na rysunku:
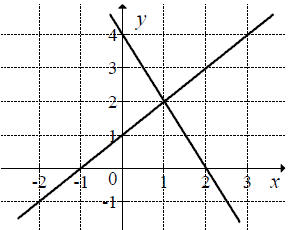
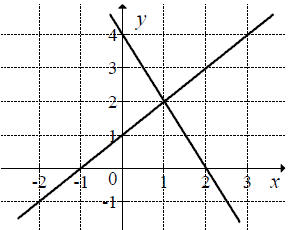
Odpowiedzi:
| A. y=x+1\wedge y=-2x+4 | B. y=x+1\wedge y=2x+4 |
| C. y=x-1\wedge y=2x+4 | D. y=x-1\wedge y=-2x+4 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10850 ⋅ Poprawnie: 110/209 [52%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Układ równań
\begin{cases}
y=-2(a+3)x-2b-6 \\
y=\frac{4}{b+3}x+a+3
\end{cases}
ma nieskończenie wiele rozwiązań dla:
Odpowiedzi:
| A. a=-5 \wedge b=-1 | B. a=-5 \wedge b=-2 |
| C. a=-4 \wedge b=-2 | D. a=-7 \wedge b=-1 |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11694 ⋅ Poprawnie: 40/101 [39%] | Rozwiąż |
Podpunkt 3.1 (0.5 pkt)
Rozwiąż układ równań metodą przeciwnych współczynników:
\begin{cases}
\frac{2}{5}x+\frac{1}{3}y=-\frac{8}{15} \\
\frac{1}{2}x-\frac{2}{9}y=-\frac{35}{18}
\end{cases}
Podaj x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 3.2 (0.5 pkt)
Podaj y.
Odpowiedź:
y=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-10868 ⋅ Poprawnie: 398/597 [66%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
» Układ równań
\begin{cases}
-2x+2y=-3 \\
-6x+6y=1
\end{cases}
:
Odpowiedzi:
| A. ma nieskończenie wiele rozwiązań | B. ma dokładnie jedno rozwiązanie |
| C. ma dokładnie dwa rozwiązania | D. jest sprzeczny |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10866 ⋅ Poprawnie: 143/231 [61%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Wskaż układ nieoznaczony:
Odpowiedzi:
| A. 8x-4y=6\ \wedge\ -6x+3y=5 | B. -5x+5y=5\ \wedge\ -2x+2y=2 |
| C. -3x-3y=6\ \wedge\ -y-x=-2 | D. -3y+3x=-2\ \wedge\ -2x+7y=3 |
| Zadanie 6. 1 pkt ⋅ Numer: pp-11701 ⋅ Poprawnie: 9/15 [60%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Wyznacz wartości parametrów m i n tak,
aby pary liczb (-8,m+10) i
(n,17) spełniały równanie
\frac{3}{10}x-\frac{1}{2}y=-\frac{17}{5}.
Podaj liczby m i n.
Odpowiedzi:
| m | = | (dwie liczby całkowite) | |
| n | = | (wpisz liczbę całkowitą) | |
| Zadanie 7. 1 pkt ⋅ Numer: pp-10951 ⋅ Poprawnie: 101/134 [75%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Sznurek o długości 31.2 metrów pocięto na trzy części,
których stosunek długości jest równy 2:4:7.
Ile decymetrów ma najdłuższa z tych części?
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 8. 1 pkt ⋅ Numer: pp-10947 ⋅ Poprawnie: 74/115 [64%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
« Statek płynie ze stałą prędkością i w ciągu minuty przepływa
730 metrów.
Zalezność przepłyniętej drogi y w kilometrach od czasu x w godzinach opisuje wzór y=a\cdot x.
Wyznacz a.
Odpowiedź:
| \frac{m}{n}= | |