⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-08-planimetria-pp-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-11566 ⋅ Poprawnie: 36/66 [54%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Kąt zewnętrzny wielokąta foremnego ma miarę 10^{\circ}.
Ile przekątnych ma ten wielokąt?
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-11462 ⋅ Poprawnie: 195/348 [56%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Trójkąt o bokach długości \sqrt{2}+1,
\sqrt{2}+1, 2\sqrt{2}, jest:
Odpowiedzi:
| A. jest ostrokątny | B. nie istnieje |
| C. jest prostokątny | D. jest rozwartokątny |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10604 ⋅ Poprawnie: 186/262 [70%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Zielone odcinki na rysunku sa równoległe, przy czym
|AD|=\frac{1}{4},
|DC|=\frac{7}{12} i
|DE|=\frac{5}{6}:
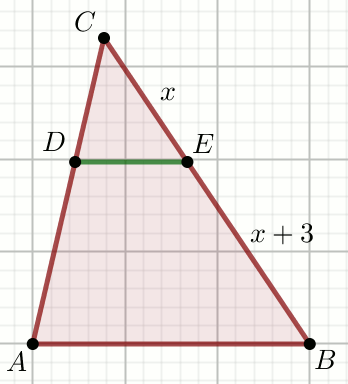
Oblicz długość odcinka AB.
Odpowiedź:
| |AB|= | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10589 ⋅ Poprawnie: 100/160 [62%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
«« Pięciokąt ABCDE jest foremny.
Który z trójkątów nie jest podobny do trójkąta ABD:
Odpowiedzi:
| A. EDB | B. ABI |
| C. BGI | D. ABG |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10590 ⋅ Poprawnie: 517/649 [79%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
«« Obwody trójkątów podobnych T_1 i
T_2 wynoszą odpowiednio 33
i 6. Najdłuższy bok trójkąta
T_2 ma długość 4.
Oblicz długość najdłuższego boku trójkąta T_1.
Odpowiedź:
| min= | |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10790 ⋅ Poprawnie: 243/369 [65%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
» Punkty o współrzędnych A=(2,-7),
B=(1,5) i C=(3,-7) są
wierzchołkami trójkąta.
Oblicz długość środkowej AD tego trójkąta.
Odpowiedź:
| |AD|= | ||
| (wpisz trzy liczby całkowite) | ||