Podgląd testu : lo2@sp-08-planimetria-pp-5
| Zadanie 1. 1 pkt ⋅ Numer: pp-10477 ⋅ Poprawnie: 369/444 [83%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Wielokąt wypukły ma 33 boków.
Wyznacz ilość przekątnych tego wielokąta.
Odpowiedź:
k=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-11560 ⋅ Poprawnie: 51/76 [67%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Które z podanych trójek są długościami boków trójkąta ostrokątnego?
Odpowiedzi:
| T/N : 12, 15, 18 | T/N : 6, 3, 3\sqrt{5} |
| T/N : 21, 21, 30 |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10595 ⋅ Poprawnie: 273/425 [64%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Zielone odcinki na rysunku sa równoległe, przy czym
|AP|=\frac{13}{12},
|BP|=\frac{13}{12} i
|CP|=\frac{13}{9}:
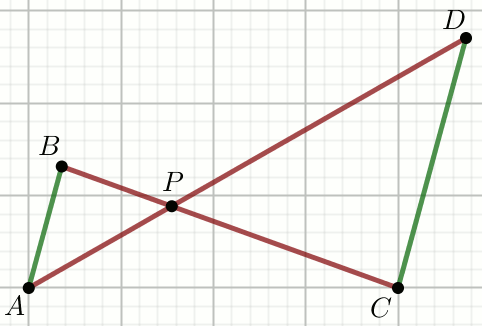

Oblicz długość odcinka DP.
Odpowiedź:
| |DP|= | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11568 ⋅ Poprawnie: 36/58 [62%] | Rozwiąż |
Podpunkt 4.1 (0.5 pkt)
W trapezie podstawy mają długość 12 i
40, a wysokość ma długość 9.
Wyznacz odległości punktu przecięcia się przekątynych tego trapezu od jego podstaw.
Podaj krótszą z tych odległości.
Odpowiedź:
| min= | |
Podpunkt 4.2 (0.5 pkt)
Podaj dłuższą z tych odległości.
Odpowiedź:
| max= | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10664 ⋅ Poprawnie: 97/158 [61%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Kąt trójkąta prostokątnego ma miarę 74^{\circ}.
Z wierzchołka kąta prostego poprowadzono środkową i wysokość tego trójkąta.
Oblicz miarę stopniową kąta między nimi.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20778 ⋅ Poprawnie: 74/249 [29%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
» W trójkącie ABC dane są:
A=(-3,4), C=(3,7).
Punkt D jest środkiem boku
AB, a
\overrightarrow{CD}=[-2, -6].
Wierzchołek B tego trójkąta ma współrzędne B=(x_B, y_B). Podaj x_B.
Odpowiedź:
x_B=
(wpisz liczbę całkowitą)
Podpunkt 6.2 (1 pkt)
Punkt E=(x_E, y_E) jest środkiem
boku BC tego trójkąta. Podaj
y_E.
Odpowiedź:
| y_E= | |
| Zadanie 7. 2 pkt ⋅ Numer: pp-20723 ⋅ Poprawnie: 101/159 [63%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
« Dane są punkty na okręgu
takie, że |AP|=3,
|PB|=\frac{11}{3} i
|CP|=\frac{1}{2}:
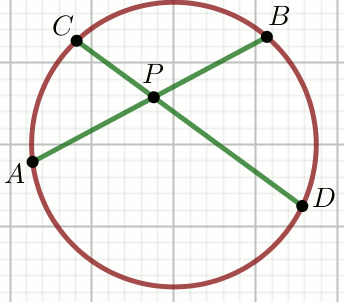

Oblicz |PD|.
Odpowiedź:
| |PD|= | |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20713 ⋅ Poprawnie: 367/726 [50%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
« Długości dwóch najkrótszych boków trójkąta prostokątnego pozostają w stosunku
15:8, a obwód tego trójkąta ma długość
400.
Wyznacz długość najkrótszego boku tego trójkąta.
Odpowiedź:
| min= | |
Podpunkt 8.2 (1 pkt)
Wyznacz długość najdłuższego boku tego trójkąta.
Odpowiedź:
| max= | |
| Zadanie 9. 3 pkt ⋅ Numer: pp-20252 ⋅ Poprawnie: 118/349 [33%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
W trójkącie ABC odcinek EF
jest symetralną boku AB oraz
|AD|=4,
|DB|=144 i
|BC|=145:
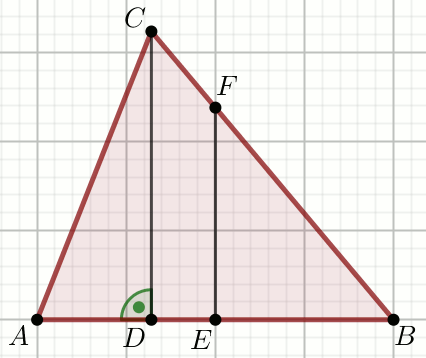

Wyznacz długości odcinków CF i FB. Podaj długość krótszego z tych odcinków.
Odpowiedź:
| min= | |
Podpunkt 9.2 (2 pkt)
Podaj długość dłuższego z tych odcinków.
Odpowiedź:
| max= | |
| Zadanie 10. 2 pkt ⋅ Numer: pp-20244 ⋅ Poprawnie: 59/154 [38%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
W trójkącie prostokątnym najkrótszy bok ma długość \frac{9}{2}, a
najdłuższy bok jest dłuższy od dłuższej przyprostokątnej o \frac{1}{2}.
Oblicz długość dłuższej przyprostokątnej tego trójkąta.
Odpowiedź:
| max= | |
Podpunkt 10.2 (1 pkt)
Oblicz odległość punktu przecięcia się środkowych tego trójkąta od
wierzchołka kąta prostego.
Odpowiedź:
| d= | |