Podgląd testu : lo2@sp-08-planimetria-pr-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-10481 ⋅ Poprawnie: 158/207 [76%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Obwód wielokąta jest równy 138. Jedna z jego przekątnych
dzieli wielokąt na dwa wielokąty o obwodach 116
i 120.
Oblicz długość tej przekątnej.
Odpowiedź:
d=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-11560 ⋅ Poprawnie: 51/76 [67%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Które z podanych trójek są długościami boków trójkąta ostrokątnego?
Odpowiedzi:
| T/N : 4\sqrt{10}, 4\sqrt{6}, 4\sqrt{5} | T/N : 4+4\sqrt{2}, -4+4\sqrt{2}, 8\sqrt{2} |
| T/N : 16, 20, 24 |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11383 ⋅ Poprawnie: 645/838 [76%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Odcinek AB o długości 12 jest
równoległy do odcinka CD, przy czym:
|PA|=20 i
|AC|=10:
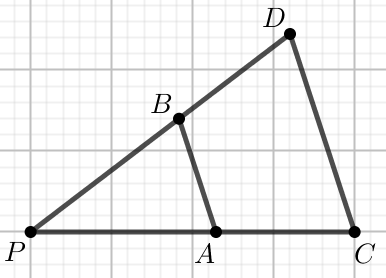

Oblicz długość odcinka CD.
Odpowiedź:
|CD|=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-11435 ⋅ Poprawnie: 330/433 [76%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Trójkąt T_1 o bokach długości
2\sqrt{23}, 3\sqrt{23} i
4\sqrt{23} jest podobny do trójkąta
T_2. Trójkąt T_2 ma boki
o długościach:
Odpowiedzi:
| A. \frac{4\sqrt{23}}{5},\frac{9\sqrt{23}}{5},\frac{8\sqrt{23}}{5} | B. \frac{6\sqrt{23}}{5},\frac{9\sqrt{23}}{5},\frac{8\sqrt{23}}{5} |
| C. \frac{4\sqrt{23}}{5},\frac{6\sqrt{23}}{5},\frac{12\sqrt{23}}{5} | D. \frac{6\sqrt{23}}{5},\frac{9\sqrt{23}}{5},\frac{12\sqrt{23}}{5} |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11510 ⋅ Poprawnie: 577/879 [65%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Punkt S=(4,3) jest środkiem odcinka
AB takiego, że punkt A=(x_A, y_A)
należy do osi Oy, a punkt B=(x_B, y_B)
należy do osi Ox.
Wyznacz współrzędne y_A i x_B.
Odpowiedzi:
| y_A | = |
(wpisz liczbę całkowitą) |
| x_B | = |
(wpisz liczbę całkowitą) |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20853 ⋅ Poprawnie: 55/757 [7%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
(2 pkt)
« W trójkącie równoramiennym ABC o podstawie
AB, wysokość AD
tworzy z jego podstawą kąt o mierze
\alpha i dzieli kąt wewnętrzny tego trójkąta przy wierzchołku
A w stosunku 1:k.
Wiedząc, że liczby k i \alpha
są naturalne dodatnie wykaż, że miara kąta \alpha
jest dzielnikiem liczby 90.
Podaj, ile rozwiązań ma to zadanie.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 7. 2 pkt ⋅ Numer: pp-20246 ⋅ Poprawnie: 80/121 [66%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
Odcinki AD i BE
przecinają się w punkcie C. W trójkątach
ABC i CDE zachodzą
związki: |\sphericalangle CAB|=|\sphericalangle CED|,
|AC|=5, |BC|=3,
|CE|=10, jak na rysunku.
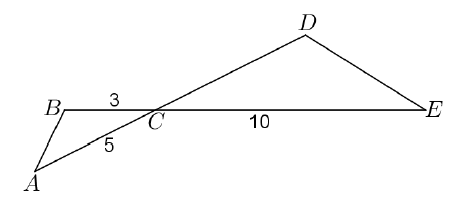

Oblicz długość boku CD.
Odpowiedź:
|CD|=
(wpisz liczbę całkowitą)
| Zadanie 8. 2 pkt ⋅ Numer: pp-20713 ⋅ Poprawnie: 367/726 [50%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
« Długości dwóch najkrótszych boków trójkąta prostokątnego pozostają w stosunku
4:3, a obwód tego trójkąta ma długość
144.
Wyznacz długość najkrótszego boku tego trójkąta.
Odpowiedź:
| min= | |
Podpunkt 8.2 (1 pkt)
Wyznacz długość najdłuższego boku tego trójkąta.
Odpowiedź:
| max= | |
| Zadanie 9. 2 pkt ⋅ Numer: pp-20251 ⋅ Poprawnie: 75/238 [31%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
« W trapezie dane są długości podstaw i ramion:
|CD|=\frac{15}{2},
|AB|=12,
|AD|=6 i
|BC|=\frac{9}{2}.
Ramiona trapezu przedłużono
do przecięcia w punkcie O.
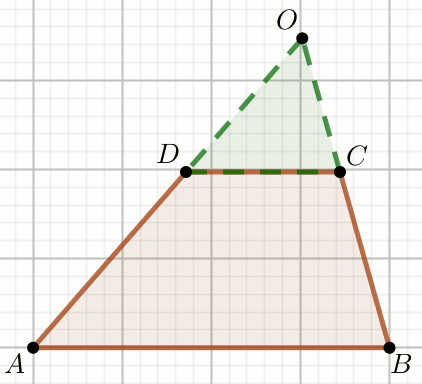
Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.

Oblicz obwód trójkąta, którego jednym z wierzchołków jest punkt O, a dwa pozostałe są końcami dłuższej podstawy trapezu.
Odpowiedź:
| L_{\triangle ABC}= | |
| Zadanie 10. 2 pkt ⋅ Numer: pp-20240 ⋅ Poprawnie: 73/182 [40%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
« Wyznacz miary kątów trójkąta pokazanego na rysunku:
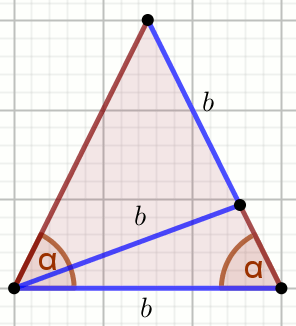

Podaj miarę stopniową najmniejszego kąta tego trójkąta.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 10.2 (1 pkt)
Podaj miarę największego kąta tego trójkąta.
Odpowiedź:
max=
(wpisz liczbę całkowitą)