⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-08-planimetria-pr-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-10479 ⋅ Poprawnie: 271/347 [78%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
W n kącie liczba przekątnych jest
16 razy większa
od liczby jego boków.
Wyznacz n.
Odpowiedź:
n=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-11560 ⋅ Poprawnie: 51/76 [67%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Które z podanych trójek są długościami boków trójkąta ostrokątnego?
Odpowiedzi:
| T/N : 3\sqrt{10}, 3\sqrt{6}, 3\sqrt{5} | T/N : 12, 15, 18 |
| T/N : 3+3\sqrt{2}, -3+3\sqrt{2}, 6\sqrt{2} |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10604 ⋅ Poprawnie: 186/263 [70%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Zielone odcinki na rysunku sa równoległe, przy czym
|AD|=\frac{2}{3},
|DC|=1 i
|DE|=\frac{5}{6}:
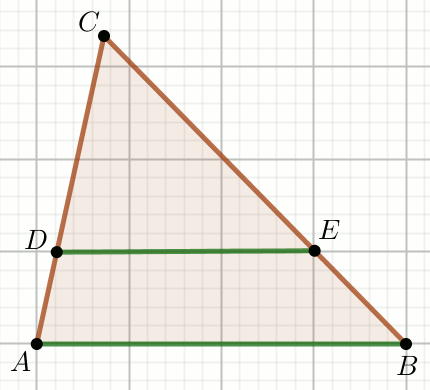
Oblicz długość odcinka AB.
Odpowiedź:
| |AB|= | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10581 ⋅ Poprawnie: 74/127 [58%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Odcinki AM i
CN są wysokościami trójkąta
ABC.
Zatem:
Odpowiedzi:
| A. |\sphericalangle CAM|=|\sphericalangle ACN| | B. |\sphericalangle BAM|=|\sphericalangle ASN| |
| C. |\sphericalangle BSN|=|\sphericalangle CAM| | D. |\sphericalangle BAM|=|\sphericalangle BCN| |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11605 ⋅ Poprawnie: 29/53 [54%] | Rozwiąż |
Podpunkt 5.1 (0.5 pkt)
Punkt S=\left(\frac{15}{2},\frac{15}{2}\right) jest punktem wspólnym odcinka
AB i jego symetralnej, przy czym
\overrightarrow{BS}=[-4,5]. Wyznacz współrzędne punktu A.
Podaj x_A.
Odpowiedź:
| x_A= | |
Podpunkt 5.2 (0.5 pkt)
Podaj y_A.
Odpowiedź:
| y_A= | |
| Zadanie 6. 2 pkt ⋅ Numer: pr-20574 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Punkty P=(x_p, y_p),
Q=(x_q, y_q) i
R=(x_r, y_r) są środkami boków odpowiednio
AB, BC i
AC trójkąta ABC.
Wierzchołek C tego trójkąta ma współrzędne
C=(x_c, y_c).
Podaj y_c.
Dane
x_p=6=6.0000000000
y_p=\frac{45}{4}=11.25000000000000
x_q=\frac{65}{4}=16.25000000000000
y_q=14=14.0000000000
x_r=\frac{33}{4}=8.25000000000000
y_r=\frac{71}{4}=17.75000000000000
y_p=\frac{45}{4}=11.25000000000000
x_q=\frac{65}{4}=16.25000000000000
y_q=14=14.0000000000
x_r=\frac{33}{4}=8.25000000000000
y_r=\frac{71}{4}=17.75000000000000
Odpowiedź:
| y_c= | |
Podpunkt 6.2 (1 pkt)
Punkt S=(x_s, y_s) jest środkiem ciężkości
tego trójkąta.
Podaj x_s.
Odpowiedź:
| x_s= | |
| Zadanie 7. 2 pkt ⋅ Numer: pr-20025 ⋅ Poprawnie: 1/2 [50%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« Wysokość prostokąta wpisanego w trójkąt o podstawie długości
6 ma długość h:
Oblicz pole powierzchni tego prostokąta.
Dane
h=2.75
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 7.2 (1 pkt)
Oblicz obwód tego prostokąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 2 pkt ⋅ Numer: pp-20241 ⋅ Poprawnie: 231/405 [57%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
W trójkącie równoramiennym
AC oraz BC są ramionami oraz.
|AC|=\sqrt{33},
|BC|=\sqrt{33} i
|AB|=6\sqrt{2}:
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
P_{\triangle}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 9. 3 pkt ⋅ Numer: pp-20252 ⋅ Poprawnie: 118/349 [33%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
W trójkącie ABC odcinek EF
jest symetralną boku AB oraz
|AD|=1,
|DB|=77 i
|BC|=85:
Wyznacz długości odcinków CF i FB. Podaj długość krótszego z tych odcinków.
Odpowiedź:
| min= | |
Podpunkt 9.2 (2 pkt)
Podaj długość dłuższego z tych odcinków.
Odpowiedź:
| max= | |
| Zadanie 10. 2 pkt ⋅ Numer: pp-20236 ⋅ Poprawnie: 105/225 [46%] | Rozwiąż |
Podpunkt 10.1 (2 pkt)
« Jedna z przyprostokątnych trójkąta prostokątnego ma długość
16, a wysokość opuszczona na przeciwprostokątną
tego trójkata długość 8\sqrt{3}.
Oblicz długość drugiej przyprostokątnej tego trójkąta.
Odpowiedź:
b=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 11. 4 pkt ⋅ Numer: pp-30022 ⋅ Poprawnie: 39/115 [33%] | Rozwiąż |
Podpunkt 11.1 (4 pkt)
« W trójkącie dane są: |AC|=50 oraz
|BC|=60. Środkowe tego trójkata AM i BN
przecinają się pod kątem prostym.
Oblicz długość boku AB tego trójkąta.
Odpowiedź:
| |AB|= | ||
| (wpisz trzy liczby całkowite) | ||