Podgląd testu : lo2@sp-09-trygonom-1-pp-4
| Zadanie 1. 1 pkt ⋅ Numer: pp-10617 ⋅ Poprawnie: 402/567 [70%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Wiadomo, że kąt \alpha jest ostry oraz
\sin\alpha=\frac{7\sqrt{53}}{53}.
Oblicz wartość wyrażenia 1+\tan\alpha\cdot\cos\alpha.
Odpowiedź:
| 1+\tan\alpha\cdot\cos\alpha= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 2. 1 pkt ⋅ Numer: pp-10652 ⋅ Poprawnie: 493/638 [77%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
W trójkącie prostokątnym długość jednej z przyprostokątnych jest równa
12, zaś długość przeciwprostokątnej jest równa
14.
Oblicz tangens mniejszego kąta ostrego w tym trójkącie.
Odpowiedź:
| \tan\alpha= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 3. 1 pkt ⋅ Numer: pp-10674 ⋅ Poprawnie: 266/707 [37%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Przekątna równoległoboku o kącie ostrym \alpha o mierze
60^{\circ} i wysokości o długości
18\sqrt{3}, tworzy kąt prosty z jego bokiem.
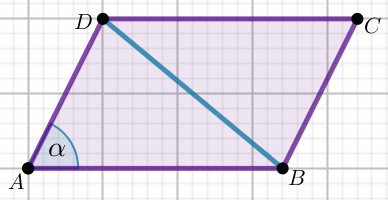

Oblicz obwód tego równoległoboku.
Odpowiedź:
L=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-10642 ⋅ Poprawnie: 327/557 [58%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Kąt \alpha jest ostry oraz
14\sin\alpha-\sqrt{3}\cos\alpha=0.
Oblicz \tan\alpha.
Odpowiedź:
| \tan\alpha= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 5. 1 pkt ⋅ Numer: pp-10615 ⋅ Poprawnie: 613/923 [66%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
a=5
b=4
« Kąt \alpha jest ostry i
\sin\alpha=\frac{\sqrt{5}}{4}.
Oblicz wartość wyrażenia 2\cos^2{\alpha}-1.
Odpowiedź:
| 2\cos^2\alpha-1= | |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20731 ⋅ Poprawnie: 133/397 [33%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
Czworokąt ABCD na rysunku jest trapezem,
a czworokąt EFCD prostokątem. Wiadomo, że
\alpha=135^{\circ}, \beta=120^{\circ} i
h=10.
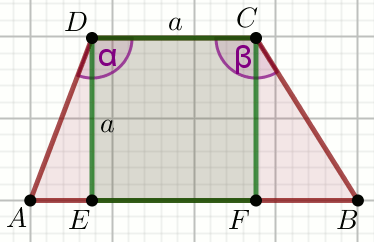

Oblicz obwód czworokąta ABCD.
Odpowiedź:
L_{ABCD}=
(liczba zapisana dziesiętnie)
| Zadanie 7. 2 pkt ⋅ Numer: pp-20728 ⋅ Poprawnie: 52/129 [40%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
W równoległoboku dany jest sinus kąta ostrego \alpha
oraz wysokość h opuszczona na dłuższy bok tego
równoległoboku. Stosunek długości sąsiednich boków tego równoległoboku
wynosi k.
Oblicz długość obwodu tego równoległoboku.
Dane
\sin\alpha=\frac{2}{5}=0.40000000000000
h=16
k=\frac{17}{2}=8.50000000000000
h=16
k=\frac{17}{2}=8.50000000000000
Odpowiedź:
| L= | |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20730 ⋅ Poprawnie: 107/257 [41%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Czworokąt na rysunku jest rombem o obwodzie długości
L:
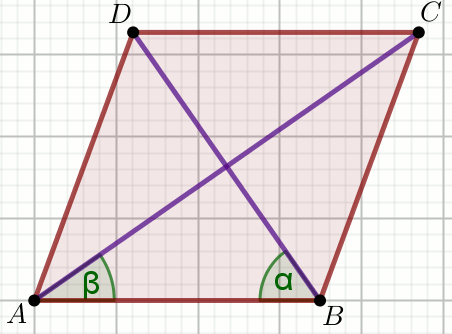

Oblicz \cos\alpha.
Dane
L=180
|DB|=54
|DB|=54
Odpowiedź:
| \cos\alpha= | |
Podpunkt 8.2 (1 pkt)
Oblicz \tan\beta.
Odpowiedź:
| \tan\beta= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 9. 2 pkt ⋅ Numer: pp-20263 ⋅ Poprawnie: 73/144 [50%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
« Podaj wartość \tan\alpha wiedząc, że
\frac{3\sin\alpha -3\cos\alpha+1}{3\sin\alpha-7\cos\alpha-4}=-\frac{1}{4}
:
Odpowiedź:
| \tan\alpha= | |
| Zadanie 10. 2 pkt ⋅ Numer: pp-20743 ⋅ Poprawnie: 73/124 [58%] | Rozwiąż |
Podpunkt 10.1 (2 pkt)
«« Kąt \alpha jest kątem ostrym oraz zachodzi
równość 6\cos^2\alpha+10\sin^2\alpha=9.
Wyznacz wartość wyrażenia w=(\tan\alpha+\cot\alpha)^2.
Odpowiedź:
| (\tan\alpha+\cot\alpha)^2= | |