Podgląd testu : lo2@sp-10-funkcje-przeksz-pp-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-10778 ⋅ Poprawnie: 649/848 [76%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Dany jest wykres funkcji y=f(x).
Aby otrzymać wykres funkcji g(x)=f(x-6)-1 wykres funkcji f należy przesunąć o wektor o współrzędnych \vec{u}=[p, q].
Podaj współrzędne p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę zapisaną dziesiętnie) |
| q | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10787 ⋅ Poprawnie: 576/910 [63%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Na rysunkach przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
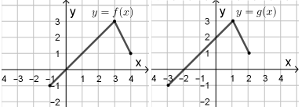
Funkcja g określona jest wzorem:

Odpowiedzi:
| A. g(x)=f(x)+2 | B. g(x)=f(x-1) |
| C. g(x)=f(x+2) | D. g(x)=f(x)-2 |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10775 ⋅ Poprawnie: 285/396 [71%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Na rysunku przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
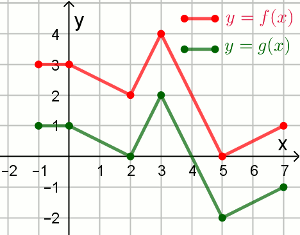
Funkcja g określona jest wzorem:

Odpowiedzi:
| A. g(x)=f(x)+2 | B. g(x)=f(x-2) |
| C. g(x)=f(x)-2 | D. g(x)=f(x+2) |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10777 ⋅ Poprawnie: 290/397 [73%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Na rysunku przedstawiony jest wykres funkcji
y=f(x).
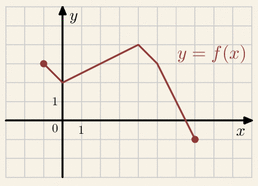
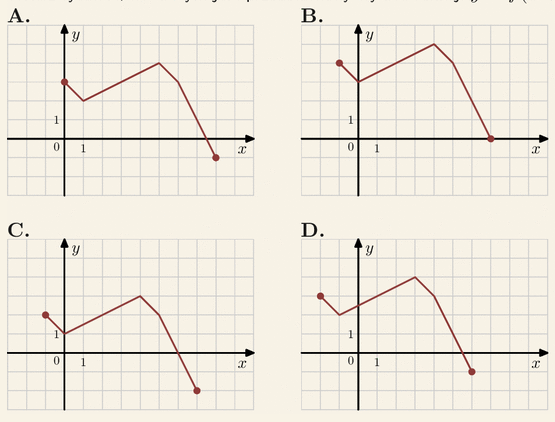

Na którym rysunku przedstawiony jest wykres funkcji y=f(x)-1:

Odpowiedzi:
| A. A | B. B |
| C. D | D. C |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11398 ⋅ Poprawnie: 266/499 [53%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« O funkcji f wiadomo, że
D_f=\langle -3,4\rangle oraz
ZW_f=\langle 2,+\infty). O funkcji
g wiadomo, że
g(x)=-f(x).
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : D_g=\langle-3,4\rangle | T/N : D_g=\langle-4,3\rangle |
| T/N : ZW_g=(-\infty,-2) |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10786 ⋅ Poprawnie: 157/277 [56%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Na rysunku 1. przedstawiono wykres funkcji
y=f(x) (czerwony), a na rysunku 2.
wykres funkcji y=g(x) (zielony):
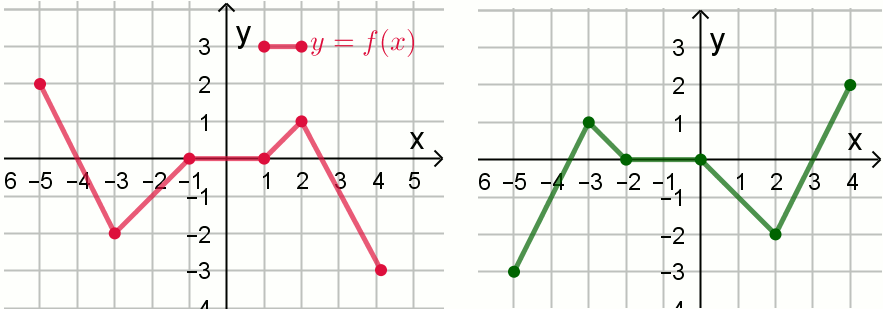
Funkcja g określona jest wzorem:
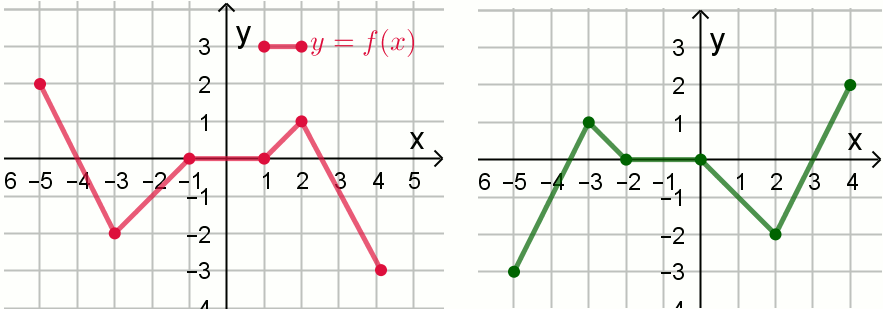
Odpowiedzi:
| A. g(x)=f(-x) | B. g(x)=f(-1-x) |
| C. g(x)=f(1-x) | D. g(x)=-f(-x) |
| Zadanie 7. 1 pkt ⋅ Numer: pp-11749 ⋅ Poprawnie: 39/44 [88%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« W wyniku przekształcenia wykresu funkcji
f(x)=2|x|-3 przez symetrię względem osi
Ox otrzymamo wykres funkcji określonej
wzorem y=a|x|+b.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 8. 1 pkt ⋅ Numer: pp-11399 ⋅ Poprawnie: 342/471 [72%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
« O funkcji f wiadomo, że
D_f=(4,6\rangle oraz
ZW_f=\langle -7,2). O funkcji
g wiadomo, że
g(x)=-f(-x). Wskaż, zdanie prawdziwe:
Odpowiedzi:
| A. D_g=(-6,-4\rangle | B. ZW_g=(-2,7\rangle |
| C. ZW_g=\langle -7,2) | D. ZW_g=\langle -2,7) |