Podgląd testu : lo2@sp-10-funkcje-przeksz-pr-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-10789 ⋅ Poprawnie: 737/1126 [65%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Na rysunku przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
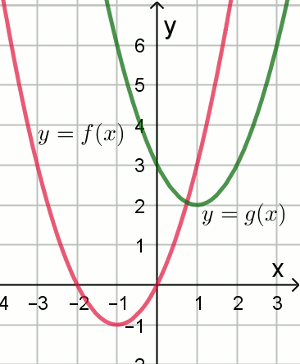
Funkcja g określona jest wzorem:

Odpowiedzi:
| A. g(x)=f(x+3)-2 | B. g(x)=f(x-2)-3 |
| C. g(x)=f(x+2)+3 | D. g(x)=f(x-2)+3 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10765 ⋅ Poprawnie: 450/659 [68%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Na rysunkach przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
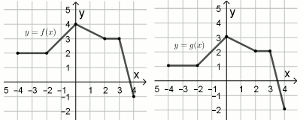
Funkcja f określona jest wzorem:

Odpowiedzi:
| A. f(x)=g(x-1)+1 | B. f(x)=g(x)+1 |
| C. f(x)=g(x+1) | D. f(x)=g(x-1)-1 |
| E. f(x)=g(x)-1 | F. f(x)=g(x-1) |
| Zadanie 3. 1 pkt ⋅ Numer: pr-10376 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Wykres funkcji określonej wzorem f(x)=\frac{x}{x+2}
przesunięto o wektor \vec{u}=[5,-4], w wyniku czego
otrzymano wykres funkcji określonej wzorem g(x)=\frac{ax+b}{x+c}.
Podaj liczby a, b i c.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| c | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10768 ⋅ Poprawnie: 204/319 [63%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji
y=f(x):
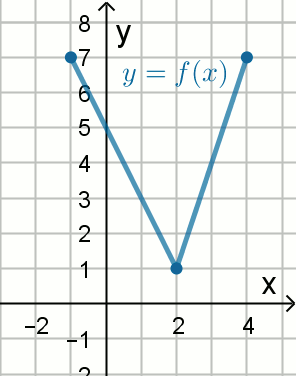
Funkcja, której wykres jest symetryczny do tego wykresu względem osi Oy określona jest wzorem:

Odpowiedzi:
| A. g(x)=f(-x) | B. y=-f(x) |
| C. y=f(-x)+1 | D. y=f(x)+1 |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10782 ⋅ Poprawnie: 175/318 [55%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji
y=f(x), której miejscem zerowym jest liczba
1 oraz f(0)=-2:
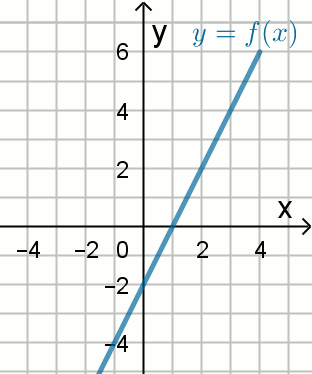
Wskaż funkcję, której wykres jest symetryczny do tego wykresu względem osi Oy:

Odpowiedzi:
| A. y=-2x-2 | B. y=2x-2 |
| C. y=2x+2 | D. y=-2x+2 |
| Zadanie 6. 1 pkt ⋅ Numer: pr-10379 ⋅ Poprawnie: 8/11 [72%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
« Funkcja f ma trzy miejsca zerowe: -3,
0 i 2, a jest zbiorem wartości jest
przedział liczbowy \langle 3,5\rangle.
Funkcja g określona jest wzorem g(x)=-f(x).
Podaj najmniejsze miejsce zerowe oraz najmniejszą wartość funkcji g.
Odpowiedzi:
| x_{min} | = |
(wpisz liczbę zapisaną dziesiętnie) |
| g_{min}(x) | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 7. 1 pkt ⋅ Numer: pr-10381 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« Wykres funkcji g jest symetryczny do wykresu
funkcji f określonej wzorem
f(x)=3(x-5)(x+4) względem początku układu współrzędnych.
Funkcja g opisana jest wzorem g(x)=ax^2+bx+c.
Podaj liczby b i c.
Odpowiedzi:
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| c | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 8. 1 pkt ⋅ Numer: pr-10382 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Zbiorem wartości funkcji określonej wzorem y=f(x) jest przedział
liczbowy \langle -7, 5\rangle, a zbiorem wartości funkcji
określonej wzorem y=|f(x)| przedział
\langle p,q\rangle.
Podaj liczby p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 9. 2 pkt ⋅ Numer: pp-20781 ⋅ Poprawnie: 172/657 [26%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
« Dane są funkcje f oraz
g, przy czym
g(x)=f(x+5)-10. O funkcji f wiadomo, że
f(3)=-1 i f(-2)=4.
Oblicz g(-2).
Odpowiedź:
g(-2)=
(wpisz liczbę całkowitą)
Podpunkt 9.2 (1 pkt)
Podaj wartość argumentu, dla którego funkcja g
przyjmuje wartość -6.
Odpowiedź:
x_0=
(wpisz liczbę całkowitą)
| Zadanie 10. 2 pkt ⋅ Numer: pp-20290 ⋅ Poprawnie: 130/346 [37%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Na rysunku przedstawiono fragment wykresu funkcji f,
który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem
y=\frac{1}{x} dla każdej liczby rzeczywistej
x\neq 0.
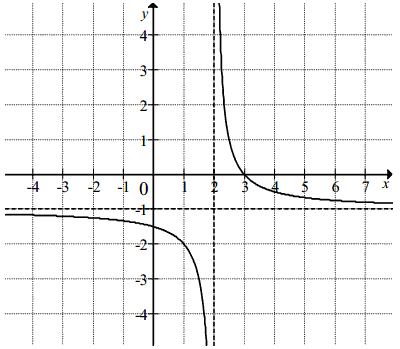

Odczytaj zbiór tych argumentów, dla których funkcja przyjmuje wartości dodatnie. Podaj liczbę występującą w środku tego zbioru.
Odpowiedź:
| Wpisz odpowiedź: | |
Podpunkt 10.2 (1 pkt)
Podaj miejsce zerowe funkcji g określonej wzorem
g(x)=f(x).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. 2 pkt ⋅ Numer: pr-20576 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 11.1 (1 pkt)
« Dziedziną funkcji f(x)=\sqrt{x} jest przedział
\langle a, b\rangle, a funkcja g
określona jest wzorem
y=g(x)=f\left(\frac{1}{4}x\right).
Wyznacz najmniejszą liczbę w zbiorze ZW_g.
Dane
a=4
b=16
b=16
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.2 (1 pkt)
Wyznacz największą liczbę w zbiorze ZW_g.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)