⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-10-funkcje-przeksz-pr-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-10778 ⋅ Poprawnie: 649/848 [76%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Dany jest wykres funkcji y=f(x).
Aby otrzymać wykres funkcji g(x)=f(x-4)+3 wykres funkcji f należy przesunąć o wektor o współrzędnych \vec{u}=[p, q].
Podaj współrzędne p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę zapisaną dziesiętnie) |
| q | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 2. 1 pkt ⋅ Numer: pr-10377 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Wykres funkcji określonej wzorem f(x)=2(x-2)(x-2)
przesunięto o wektor \vec{u}=[-5,-9], w wyniku czego
otrzymano wykres funkcji określonej wzorem g(x)=ax^2+bx+c.
Podaj liczby a, b i c.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| c | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10783 ⋅ Poprawnie: 409/519 [78%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Na rysunku 1. jest przedstawiony wykres funkcji f,
a na rysunku 2. – wykres funkcji g.
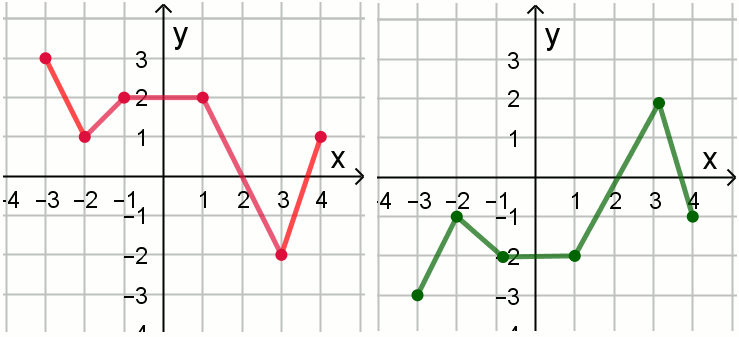
Funkcja g jest określona wzorem:
Odpowiedzi:
| A. g(x)=-f(x) | B. g(x)=f(x)+4 |
| C. g(x)=f(-x) | D. g(x)=f(x)-4 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11399 ⋅ Poprawnie: 342/471 [72%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« O funkcji f wiadomo, że
D_f=(-7,-5\rangle oraz
ZW_f=\langle -1,4). O funkcji
g wiadomo, że
g(x)=-f(-x). Wskaż, zdanie prawdziwe:
Odpowiedzi:
| A. ZW_g=\langle -1,4) | B. D_g=(5,7\rangle |
| C. ZW_g=(-4,1\rangle | D. ZW_g=\langle -4,1) |
| Zadanie 5. 1 pkt ⋅ Numer: pr-10289 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 5.1 (1 pkt)
O funkcji f wiadomo, że ma trzy miejsca zerowe
-3, 12 i
14.
Wyznacz sumę miejsc zerowych funkcji g określonej wzorem g(x)=|f(x)|.
Odpowiedź:
suma=
(wpisz liczbę całkowitą)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20781 ⋅ Poprawnie: 172/657 [26%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
« Dane są funkcje f oraz
g, przy czym
g(x)=f(x+5)-10. O funkcji f wiadomo, że
f(3)=9 i f(-2)=6.
Oblicz g(-2).
Odpowiedź:
g(-2)=
(wpisz liczbę całkowitą)
Podpunkt 6.2 (1 pkt)
Podaj wartość argumentu, dla którego funkcja g
przyjmuje wartość -4.
Odpowiedź:
x_0=
(wpisz liczbę całkowitą)
| Zadanie 7. 2 pkt ⋅ Numer: pp-20296 ⋅ Poprawnie: 47/160 [29%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
» Dana jest funkcja f(x)=\frac{2639}{x}, gdzie
x\neq 0. Jej wykres przesunięto wzdłuż osi
Oy i otrzymano wykres funkcji
y=g(x), do którego należy punkt
B=(29,105). Wyznacz wektor tego przesunięcia
\vec{u}=[u_x,u_y].
Podaj u_y.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 7.2 (1 pkt)
Ile liczb naturalnych k ze zbioru
\{0,1,2,3,...,148\} ma tę własność, że liczba
g(k) jest całkowita?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 2 pkt ⋅ Numer: pr-20576 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 8.1 (1 pkt)
« Dziedziną funkcji f(x)=\sqrt{x} jest przedział
\langle a, b\rangle, a funkcja g
określona jest wzorem
y=g(x)=f\left(\frac{1}{4}x\right).
Wyznacz najmniejszą liczbę w zbiorze ZW_g.
Dane
a=9
b=25
b=25
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.2 (1 pkt)
Wyznacz największą liczbę w zbiorze ZW_g.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. 2 pkt ⋅ Numer: pr-20894 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Dziedziną funkcji f jest przedział liczbowy
(-6,5), a zbiorem jej wartości przedział
(-5,3). Funkcja g
określona jest wzorem g(x)=-\frac{4}{3}f(x).
Dziedziną funkcji g jest zbiór D_g=(x_1,x_2).
Dziedziną funkcji g jest zbiór D_g=(x_1,x_2).
Podaj liczby x_1 i x_2.
Odpowiedzi:
| x_1 | = |
(wpisz liczbę zapisaną dziesiętnie) |
| x_2 | = |
(wpisz liczbę zapisaną dziesiętnie) |
Podpunkt 9.2 (1 pkt)
Zbiorem wartości funkcji g jest zbiór
ZW_g=(y_1,y_2).
Podaj liczby y_1 i y_2.
Odpowiedzi:
| y_1 | = |
(wpisz liczbę zapisaną dziesiętnie) |
| y_2 | = |
(wpisz liczbę zapisaną dziesiętnie) |