Podgląd testu : lo2@sp-12-funkcja-kwadratowa-pp-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-11643 ⋅ Poprawnie: 95/193 [49%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Do wykresu funkcji kwadratowej określonej wzorem y=x^2+bx+c
należą punkty o współrzędnych (10,3) i
(3,-18).
Wyznacz współczynniki b i c.
Odpowiedzi:
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10990 ⋅ Poprawnie: 263/409 [64%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Funkcja f(x)=x^2-26x+169
dla argumentu \sqrt{13} przyjmuje wartość
\left(......\cdot\sqrt{13}-13\right)^2.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-11044 ⋅ Poprawnie: 142/223 [63%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Wykres funkcji kwadratowej g przecina oś
Ox w dwóch punktach.
Funkcja g opisana jest wzorem:
Odpowiedzi:
| A. g(x)=4(x+5)^2+4 | B. g(x)=-12(x-11)^2+\sqrt{11} |
| C. g(x)=7(x+7)^2+14 | D. g(x)=-2(x+11)^2-11 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11078 ⋅ Poprawnie: 196/346 [56%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Dana jest funkcja f(x)=-5(x+11)(x-6).
Wyznacz maksymalny przedział, w którym funkcja f jest
rosnąca.
Podaj mniejszy z końców liczbowych tego przedziału.
Odpowiedź:
| min= | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11026 ⋅ Poprawnie: 241/318 [75%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Dana jest funkcja g:\mathbb{R}\to\mathbb{R} określona wzorem
g(x)=x^2-3+2x.
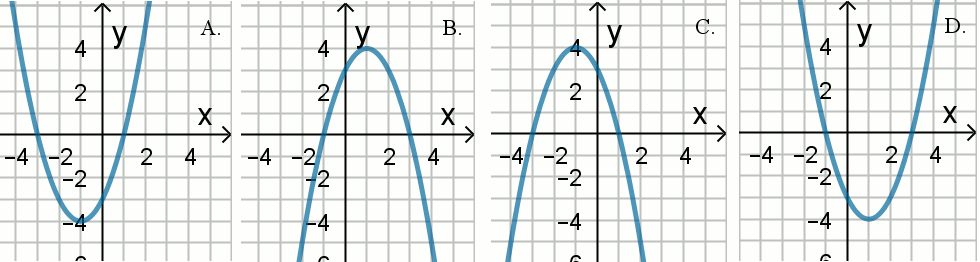

Wykres funkcji g przedstawia rysunek:
Odpowiedzi:
| A. A | B. C |
| C. D | D. B |
| Zadanie 6. 1 pkt ⋅ Numer: pp-11043 ⋅ Poprawnie: 148/269 [55%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Liczba punktów wspólnych wykresu funkcji
h(x)=2x^2+\frac{7}{3}x+\frac{2}{9} z osiami układu
współrzędnych jest równa:
Odpowiedzi:
| A. 2 | B. 0 |
| C. 1 | D. 3 |
| Zadanie 7. 1 pkt ⋅ Numer: pp-11465 ⋅ Poprawnie: 481/946 [50%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
» Najmniejszą wartość w przedziale
\langle -13, -9\rangle funkcja kwadratowa
f(x)=-\left(x+12\right)^{2}-5
przyjmuje dla argumentu ......... .
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 8. 1 pkt ⋅ Numer: pp-11067 ⋅ Poprawnie: 144/278 [51%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
« Rozpatrujemy prostokąty o obwodzie 12. Na takim
prostokącie o największym polu powierzchni opisano okrąg.
Oblicz długość promienia tego okręgu.
Odpowiedź:
| R= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 9. 1 pkt ⋅ Numer: pp-10971 ⋅ Poprawnie: 132/197 [67%] | Rozwiąż |
Podpunkt 9.1 (0.2 pkt)
Równanie x^2-(k-6)x+4=0 z niewiadomą
x ma dwa różne rozwiązania wtedy i tylko wtedy, gdy parametr
k należy do zbioru A. Zapisz zbiór
Aw postaci sumy przedziałów.
Zbiór A jest postaci:
Odpowiedzi:
| A. (p,+\infty) | B. (-\infty,p) |
| C. (-\infty,p)\cup(q,+\infty) | D. (p,q) |
| E. \langle p,q\rangle | F. (-\infty,p)\cap(q,+\infty) |
Podpunkt 9.2 (0.8 pkt)
Liczba p jest najmniejszym, a liczba q
największym z końców liczbowych tych przedziałów.
Podaj liczby p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 10. 1 pkt ⋅ Numer: pp-10965 ⋅ Poprawnie: 538/882 [60%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Wskaż te nierówności, których rozwiązaniem jest zbiór \mathbb{R}:
Odpowiedzi:
| T/N : 2x^2+6x+4 \geqslant 0 | T/N : x^2+x+\frac{1}{4} > 0 |