Podgląd testu : lo2@sp-12-funkcja-kwadratowa-pp-4
| Zadanie 1. 1 pkt ⋅ Numer: pp-11074 ⋅ Poprawnie: 94/159 [59%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Różnica iloczynu liczby 12 oraz liczby x i kwadratu liczby
xjest największa dla liczby x równej:
Odpowiedź:
| x= | |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11013 ⋅ Poprawnie: 1054/1531 [68%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Trójmian kwadratowy
y=2x^2+2x-4 można zapisać w postaci
y=a(x+2)(x-m).
Wyznacz wartości parametrów a i m.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| m | = |
(wpisz liczbę całkowitą) |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11024 ⋅ Poprawnie: 121/339 [35%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Na rysunku pokazano tylko część wykresu funkcji
f(x)=ax^2+bx+c, dla której
D_f=\mathbb{R}.
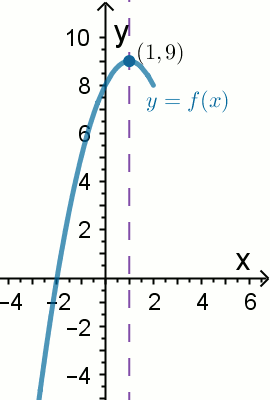

Wówczas:
Odpowiedzi:
| T/N : funkcja jest rosnąca w przedziale (-2, 4) | T/N : funkcja przyjmuje wartości większe od zera dla x \lessdot 1 |
| T/N : miejscami zerowymi tej funkcji są liczby -2 i 4 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11409 ⋅ Poprawnie: 223/340 [65%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Na rysunku przedstawiono wykres funkcji kwadratowej f:
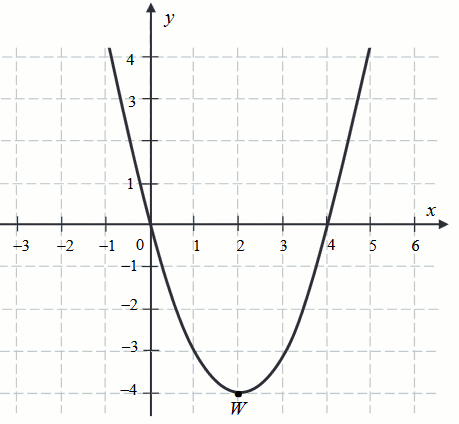

Podaj największą wartość funkcji f w przedziale \langle 1,4\rangle.
Odpowiedź:
f_{max}(x)=
(wpisz liczbę całkowitą)
| Zadanie 5. 1 pkt ⋅ Numer: pp-10961 ⋅ Poprawnie: 399/726 [54%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« Suma wszystkich rozwiązań całkowitych nierówności
(8-x)(x+4)\geqslant 0
jest równa ......... .
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20929 ⋅ Poprawnie: 39/58 [67%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Funkcja kwadratowa f określona wzorem
f(x)=a(x-p)^2+q dla argumentu
3 osiąga wartość najmniejszą równą
-1. Wiedząc, że do jej wykresu należy punkt
należy punkt A=(4,4), wyznacz wzór tej funkcji.
Podaj współczynnik a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 6.2 (1 pkt)
Podaj liczby p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 7. 2 pkt ⋅ Numer: pp-20936 ⋅ Poprawnie: 51/143 [35%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Funkcja kwadratowa określona wzorem f(x)=-x^2+bx+c
jest malejąca wtedy i tylko wtedy, gdy x\in\langle 1,+\infty).
Wiedząc, że f(-2)=-4, oblicz współczynniki
b i c.
Podaj liczbę b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
Podpunkt 7.2 (1 pkt)
Podaj liczbę c.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
| Zadanie 8. 2 pkt ⋅ Numer: pp-20941 ⋅ Poprawnie: 130/224 [58%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Wiadomo, że x-y=62, a także, że suma x^2+y^2
jest najmniejsza możliwa.
Podaj liczbę x.
Odpowiedź:
x=
(wpisz liczbę całkowitą)
Podpunkt 8.2 (1 pkt)
Podaj liczbę y.
Odpowiedź:
y=
(wpisz liczbę całkowitą)
| Zadanie 9. 2 pkt ⋅ Numer: pp-20394 ⋅ Poprawnie: 15/176 [8%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
« Rozwiąż nierówność x^2+bx+c \lessdot 0.
Ile liczb całkowitych z przedziału \langle -10, 10\rangle spełnia tę nierówność?
Dane
b=-\frac{10}{3}=-3.33333333333333
c=1=1.00000000000000
c=1=1.00000000000000
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
Podpunkt 9.2 (1 pkt)
Zbiór rozwiązań zapisz w postaci sumy przedziałów. Podaj współrzędną punktu,
względem którego zbiór ten jest symetryczny.
Odpowiedź:
| x_s= | |