Podgląd testu : lo2@sp-12-funkcja-kwadratowa-pp-5
| Zadanie 1. 1 pkt ⋅ Numer: pp-11060 ⋅ Poprawnie: 134/185 [72%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Wierzchołek paraboli o równaniu y=(x+6)^2+2m-1
należy do prostej o równaniu y=3.
Wyznacz wartość parametru m.
Odpowiedź:
| m= | |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11506 ⋅ Poprawnie: 461/803 [57%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Osią symetrii paraboli będącej wykresem funkcji kwadratowej określonej równaniem
f(x)=-\frac{1}{2}(x-108)(x+324), jest prosta określona:
równaniem x-......=0.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-11022 ⋅ Poprawnie: 76/227 [33%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Rysunek przedstawia wykres funkcji kwadratowej
h(x)=a(x+b)^2+c.
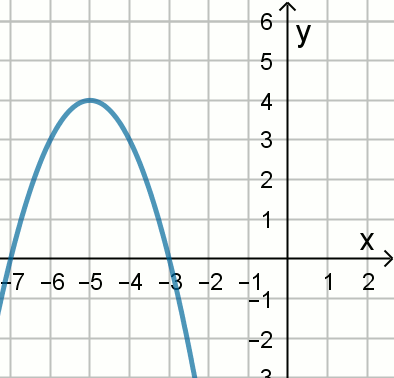

Zatem:
Odpowiedzi:
| A. c=-5 | B. c=5 |
| C. b=5 | D. b=-5 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11730 ⋅ Poprawnie: 27/45 [60%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Większa część zawodników klubu sportowego liczącego 57 osób,
zachorowała na grypę. Każdy zdrowy zawodnik postanowił wysłać każdemu choremu kartkę z
pozdrowieniami. Liczba wszystkich wysłanych kartek była największa możliwa.
Ilu zawodników było chorych?
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 5. 1 pkt ⋅ Numer: pp-10958 ⋅ Poprawnie: 251/430 [58%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
«« Najmniejszą liczbą całkowitą należącą do dziedziny funkcji
f(x)=\sqrt{-x^2-\frac{3}{2}x+\frac{5}{2}}
jest ......... .
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20342 ⋅ Poprawnie: 75/123 [60%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
» Wykres funkcji f(x)=x^2+4x+c-15 jest styczny do osi
Ox.
Wyznacz c.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
| Zadanie 7. 2 pkt ⋅ Numer: pp-20935 ⋅ Poprawnie: 14/23 [60%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Średnia arytmetyczna miejsc zerowych funkcji kwadratowej określonej wzorem f(x)=ax^2+bx
jest równa 2. Rzędna wierzchołka paraboli będącej
wykresem tej funkcji jest równa -8.
Wyznacz współczynnik a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 7.2 (1 pkt)
Wyznacz współczynnik b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 8. 2 pkt ⋅ Numer: pp-20363 ⋅ Poprawnie: 175/370 [47%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
« Dana jest funkcja f(x)=x^2+bx+c, gdzie
x\in\langle p, q\rangle.
Oblicz najmniejszą wartość funkcji f.
Dane
b=-2
c=0
p=-1
q=2
c=0
p=-1
q=2
Odpowiedź:
f_{min}(x)=
(wpisz liczbę całkowitą)
Podpunkt 8.2 (1 pkt)
Oblicz największą wartość funkcji f.
Odpowiedź:
f_{max}(x)=
(wpisz liczbę całkowitą)
| Zadanie 9. 2 pkt ⋅ Numer: pp-20377 ⋅ Poprawnie: 67/114 [58%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Wyznacz punkty przecięcia paraboli określonej wzorem y=2x^2+33x+14
z prostą o równaniu y=-2.
Podaj najmniejszą możliwą współrzędną punktu przecięcia się obu wykresów.
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 9.2 (1 pkt)
Podaj największą możliwą współrzędną punktu przecięcia się obu wykresów.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 10. 2 pkt ⋅ Numer: pp-20418 ⋅ Poprawnie: 88/226 [38%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Rozwiąż nierówność
x^2+2ax-2(x+a)+a^2 \geqslant \frac{1}{3}(a+x-2)(a+x-8)
.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj średnią arytmetyczną wszystkich końców liczbowych tych przedziałów.
Dane
a=1
Odpowiedź:
| s= | |
Podpunkt 10.2 (1 pkt)
Podaj sumę wszystkich końców liczbowych tych przedziałów.
Odpowiedź:
suma=
(wpisz liczbę całkowitą)
| Zadanie 11. 4 pkt ⋅ Numer: pp-30079 ⋅ Poprawnie: 22/92 [23%] | Rozwiąż |
Podpunkt 11.1 (2 pkt)
« Liczba c jest rozwiązaniem równania
8^{p}+2^{q}\cdot x=0, zaś liczba
d wynosi
\frac{125^{500}}{5^{1500}}.
Funkcja kwadratowa g(x)=(x-c)(x-d) określona jest
w przedziale \langle x_1,x_2\rangle.
Podaj najmniejszą wartość funkcji g.
Dane
p=21
q=60
x1=-4
x2=0
q=60
x1=-4
x2=0
Odpowiedź:
| min= | |
Podpunkt 11.2 (2 pkt)
Podaj największą wartość funkcji g.
Odpowiedź:
g_{max}(x)=
(wpisz liczbę całkowitą)