Podgląd testu : lo2@sp-12-funkcja-kwadratowa-pp-6
| Zadanie 1. 1 pkt ⋅ Numer: pp-11031 ⋅ Poprawnie: 419/591 [70%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Wierzchołkiem paraboli, która jest wykresem funkcji f
jest punkt W=(-8,1).
Wówczas:
Odpowiedzi:
| T/N : f(-16)=f(-1) | T/N : f(-13)=f(-2) |
| T/N : f(-18)=f(2) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11041 ⋅ Poprawnie: 367/696 [52%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Wyznacz największa wartość funkcji określonej wzorem
y=-2(x+7)(x+8).
Odpowiedź:
| y_{max}= | |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11534 ⋅ Poprawnie: 216/314 [68%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
(1 pkt)
Jeden z poniższych wzorów opisuje funkcję postaci
y=ax^2+bx+c, której wykres pokazano na rysunku:
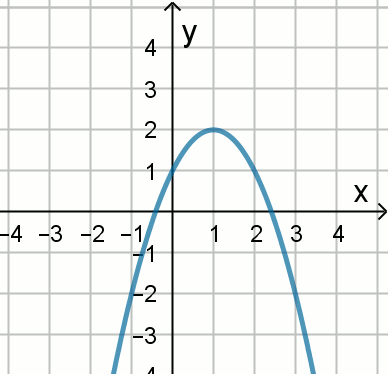

Wskaż ten wzór:
Odpowiedzi:
| A. y=a(x-2)^2+1 | B. y=a(x+1)^2+2 |
| C. y=a(x-1)^2+2 | D. y=a(x-1)^2-2 |
| E. y=a(x+1)^2-2 | F. y=a(x-2)^2-1 |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10978 ⋅ Poprawnie: 475/746 [63%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Najmniejszą wartość w przedziale
\langle -11, -7\rangle funkcja kwadratowa
określona wzorem
f(x)=-\left(x+8\right)^{2}+5
przyjmuje dla argumentu ......... .
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 5. 1 pkt ⋅ Numer: pp-10961 ⋅ Poprawnie: 399/726 [54%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« Suma wszystkich rozwiązań całkowitych nierówności
(-6-5x)(x+7)\geqslant 0
jest równa ......... .
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
| Zadanie 6. 3 pkt ⋅ Numer: pp-20841 ⋅ Poprawnie: 60/101 [59%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
» Wyznacz współczynniki b i c
funkcji określonej wzorem f(x)=4x^2+bx+c wiedząc, że zbiorem jej wartości
jest przedział \langle -6,+\infty), a osią symetrii jej
wykresu jest prosta x=-5.
Podaj b.
Odpowiedź:
| b= | |
Podpunkt 6.2 (1 pkt)
Podaj c.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
| Zadanie 7. 2 pkt ⋅ Numer: pp-20937 ⋅ Poprawnie: 69/138 [50%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Osią symetrii paraboli będącej wykresem funkcji kwadratowej określonej wzorem
f(x)=3x^2+bx+c jest prosta o równaniu x=6,
a najmniejszą wartością tej funkcji jest -11.
Wyznacz współczynnik b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
Podpunkt 7.2 (1 pkt)
Wyznacz współczynnik c.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
| Zadanie 8. 2 pkt ⋅ Numer: pp-20365 ⋅ Poprawnie: 84/186 [45%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
« Dana jest funkcja f(x)=ax^2+bx+c.
Oblicz najmniejszą wartość funkcji f w przedziale \langle p, q\rangle.
Dane
a=-1
b=6
c=-4
p=2
q=7
b=6
c=-4
p=2
q=7
Odpowiedź:
f_{min}(x)=
(wpisz liczbę całkowitą)
| Zadanie 9. 2 pkt ⋅ Numer: pp-20782 ⋅ Poprawnie: 61/83 [73%] | Rozwiąż |
Podpunkt 9.1 (1 pkt)
Dane jest równanie (x^3+27)(x^2-x-42)=0.
Wyznacz najmniejsze rozwiązanie tego równania.
Odpowiedź:
| x_{min}= |
|
|
| (wpisz cztery liczby całkowite) | ||
Podpunkt 9.2 (1 pkt)
Wyznacz największe rozwiązanie tego równania.
Odpowiedź:
| x_{max}= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 10. 2 pkt ⋅ Numer: pp-20418 ⋅ Poprawnie: 88/226 [38%] | Rozwiąż |
Podpunkt 10.1 (1 pkt)
Rozwiąż nierówność
x^2+2ax-2(x+a)+a^2 \geqslant \frac{1}{3}(a+x-2)(a+x-8)
.
Rozwiązanie zapisz w postaci sumy przedziałów. Podaj średnią arytmetyczną wszystkich końców liczbowych tych przedziałów.
Dane
a=-3
Odpowiedź:
| s= | |
Podpunkt 10.2 (1 pkt)
Podaj sumę wszystkich końców liczbowych tych przedziałów.
Odpowiedź:
suma=
(wpisz liczbę całkowitą)
| Zadanie 11. 4 pkt ⋅ Numer: pp-30076 ⋅ Poprawnie: 40/81 [49%] | Rozwiąż |
Podpunkt 11.1 (2 pkt)
Miejscami zerowymi funkcji f(x)=-\frac{1}{2}x^2+bx+c
są liczby 2 i 10.
Naszkicuj wykres funkcji f.
Oblicz c.
Odpowiedź:
c=
(wpisz liczbę całkowitą)
Podpunkt 11.2 (1 pkt)
Wykres funkcji f leży powyżej wykresu
funkcji g(x)=x-2 wtedy i tylko wtedy, gdy
x\in(p, q).
Podaj p.
Odpowiedź:
p=
(wpisz liczbę całkowitą)
Podpunkt 11.3 (1 pkt)
Podaj q.
Odpowiedź:
q=
(wpisz liczbę całkowitą)
| Zadanie 12. 4 pkt ⋅ Numer: pp-30083 ⋅ Poprawnie: 62/220 [28%] | Rozwiąż |
Podpunkt 12.1 (2 pkt)
« Ze sznurka o długości d cm zrobiono dwa
prostokąty P_1 i P_2.
W prostokącie P_1 jeden z boków jest dwukrotnie
dłuższy od drugiego, zaś w prostokącie P_2 jeden bok
jest czterokrotnie krótszy od boku drugiego.
Wówczas okazało się, że suma pól powierzchni obu prostokątów
P_1 i P_2 była najmniejsza
z możliwych.
Podaj długość krótszego boku prostokąta P_1.
Dane
d=43
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 12.2 (2 pkt)
Podaj długość krótszego boku prostokąta P_2.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 13. 4 pkt ⋅ Numer: pp-30096 ⋅ Poprawnie: 22/46 [47%] | Rozwiąż |
Podpunkt 13.1 (4 pkt)
Zbiornik wody, którego objetość wynosi 2574
m3 można napełnić wodą lecącą z dwóch kranów. Pierwszy kran napełnia
zbiornik w czasie t_1=286 godzin, natomiast drugi w
czasie t_2=198 godzin. W ciągu jednej godziny przez kran pierwszy
przelatuje o 4 m3 wody mniej niż przez
kran drugi.
Ile godzin potrwa napełnianianie pustego zbiornika jeśli wodę będą dostarczały obia krany?
Odpowiedź:
ile\ [h]=
(wpisz liczbę całkowitą)