⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-13-okr-i-kola-pp-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-10546 ⋅ Poprawnie: 630/964 [65%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Punkt O jest środkiem okręgu na rysunku, w którym
\alpha=44^{\circ}:
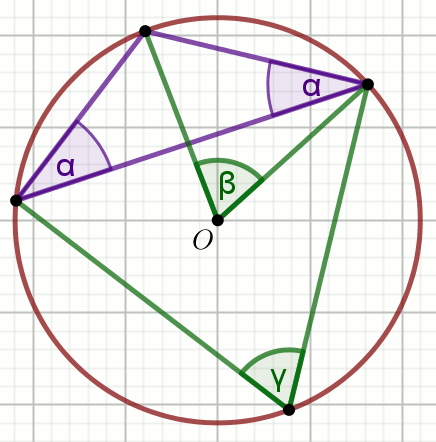
Wyznacz miary stopniowe kątów \beta i \gamma.
Odpowiedzi:
| \beta | = |
(wpisz liczbę całkowitą) |
| \gamma | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10491 ⋅ Poprawnie: 57/76 [75%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« W kąt \alpha o mierze 58^{\circ} wpisano okrąg o środku
O styczny do ramion kąta w punktach
A i B.
Wyznacz miarę stopniową mniejszego z kątów środkowych okręgu AOB.
Odpowiedź:
|\sphericalangle AOB|=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10523 ⋅ Poprawnie: 67/108 [62%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Punkt O jest środkiem okręgu, a kąt \alpha
ma miarę 69^{\circ}:
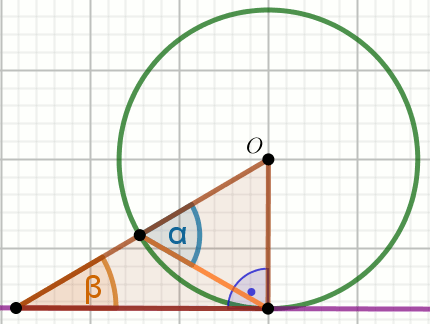
Wyznacz miarę stopniową kąta \beta zaznaczonego na rysunku.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pp-10525 ⋅ Poprawnie: 58/101 [57%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Punkt O jest środkiem okręgu, przy czym
\alpha=138^{\circ}:
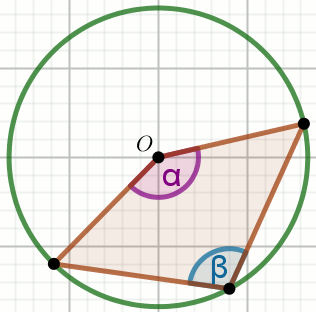
Wyznacz miarę stopniową kąta \beta.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 5. 1 pkt ⋅ Numer: pp-11655 ⋅ Poprawnie: 25/43 [58%] | Rozwiąż |
Podpunkt 5.1 (0.5 pkt)
Okręgi o_1(A, r_1) oraz o_2(B,r_2)
(r_1\lessdot r_2) są styczne wewnętrznie, a odległość ich środków jest równa \frac{5}{2}.
Suma długości promieni tych okręgów jest równa \frac{9}{2}.
Oblicz r_1.
Odpowiedź:
| r_1= | |
Podpunkt 5.2 (0.5 pkt)
Oblicz r_2.
Odpowiedź:
| r_2= | |
| Zadanie 6. 1 pkt ⋅ Numer: pp-10564 ⋅ Poprawnie: 131/190 [68%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
Dwa okręgi mają promienie o długości \frac{5}{6} i
\frac{13}{6}. Mniejszy z okręgów przechodzi przez środek
większego.
Oblicz odległość między środkami tych okręgów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 1 pkt ⋅ Numer: pp-11649 ⋅ Poprawnie: 33/60 [55%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
W okręgu o promieniu 90 narysowano cięciwę,
która znajduje się w odległości 54
od środka tego okręgu.
Oblicz długość tej cięciwy.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)