⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-13-okr-i-kola-pp-4
| Zadanie 1. 1 pkt ⋅ Numer: pp-10546 ⋅ Poprawnie: 630/964 [65%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Punkt O jest środkiem okręgu na rysunku, w którym
\alpha=44^{\circ}:
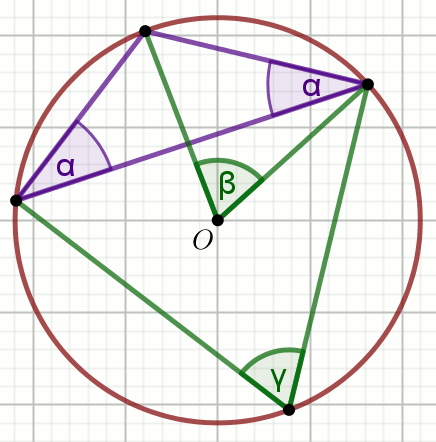
Wyznacz miary stopniowe kątów \beta i \gamma.
Odpowiedzi:
| \beta | = |
(wpisz liczbę całkowitą) |
| \gamma | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10523 ⋅ Poprawnie: 67/108 [62%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Punkt O jest środkiem okręgu, a kąt \alpha
ma miarę 69^{\circ}:
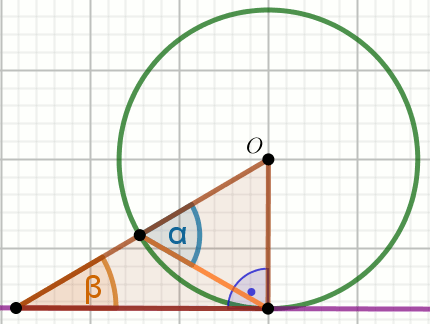
Wyznacz miarę stopniową kąta \beta zaznaczonego na rysunku.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-11737 ⋅ Poprawnie: 6/10 [60%] | Rozwiąż |
Podpunkt 3.1 (0.5 pkt)
Okręgi o_1(A, r_1) oraz o_2(B,r_2)
(r_1\lessdot r_2) są styczne zewnętrznie, a odległość ich środków jest równa \frac{32}{3}.
Stosunek długości promieni tych okręgów jest równy 7.
Oblicz r_1.
Odpowiedź:
| r_1= | |
Podpunkt 3.2 (0.5 pkt)
Oblicz r_2.
Odpowiedź:
| r_2= | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11739 ⋅ Poprawnie: 28/30 [93%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Jaką część okręgu o promieniu 3
stanowi jego łuk o długości 7\pi?
Odpowiedź:
| \frac{m}{n}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 5. 2 pkt ⋅ Numer: pp-20203 ⋅ Poprawnie: 50/101 [49%] | Rozwiąż |
Podpunkt 5.1 (2 pkt)
Brązowy czworokąt na rysunku jest prostokątem:
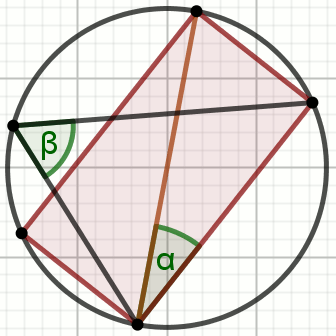
Oblicz miarę stopniową kąta \alpha.
Dane
\beta=66^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20221 ⋅ Poprawnie: 21/43 [48%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
Na okręgu o środku O zaznaczono dwa punkty
A i B, które podzieliły
ten okrąg na dwa łuki, których długości pozostają w stosunku
a:b.
Oblicz miarę stopniową mniejszego z kątów środkowych AOB tego okręgu.
Dane
a:b=\frac{4}{5}=0.80000000000000
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)