Podgląd testu : lo2@sp-13-okr-i-kola-pp-5
| Zadanie 1. 1 pkt ⋅ Numer: pp-10548 ⋅ Poprawnie: 276/537 [51%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Punkt O jest środkiem okręgu na rysunku, w którym
\alpha=52^{\circ}:
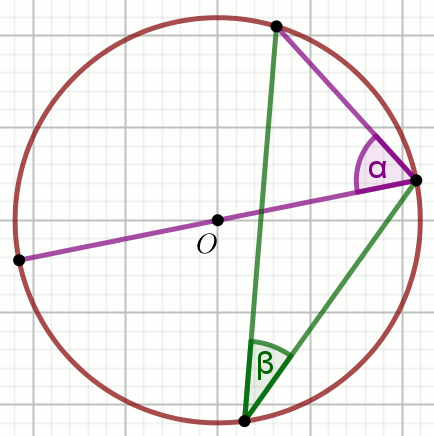

Oblicz miarę stopniową kąta \beta.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10538 ⋅ Poprawnie: 139/246 [56%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Punkt O jest środkiem okręgu:
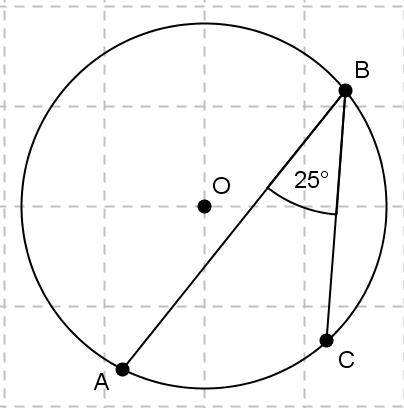

Wyznacz miarę stopniową kąta ACO.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 1 pkt ⋅ Numer: pp-11738 ⋅ Poprawnie: 34/52 [65%] | Rozwiąż |
Podpunkt 3.1 (0.5 pkt)
Okręgi o_1(A, r_1) oraz o_2(B,r_2)
(r_1\lessdot r_2) są styczne wewnętrznie, a odległość ich środków jest równa 9.
Stosunek długości promieni tych okręgów jest równy 4.
Oblicz r_1.
Odpowiedź:
| r_1= | |
Podpunkt 3.2 (0.5 pkt)
Oblicz r_2.
Odpowiedź:
| r_2= | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11739 ⋅ Poprawnie: 28/30 [93%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Jaką część okręgu o promieniu 2
stanowi jego łuk o długości 7\pi?
Odpowiedź:
| \frac{m}{n}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 5. 2 pkt ⋅ Numer: pp-20226 ⋅ Poprawnie: 43/93 [46%] | Rozwiąż |
Podpunkt 5.1 (2 pkt)
W okręgu o środku O i promieniu długości
r poprowadzono dwie równoległe cięciwy
AB i CD położone
po tej samej stronie środka okręgu:
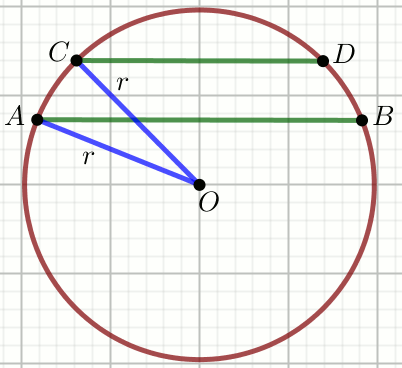

Oblicz odległość pomiędzy tymi cięciwami.
Dane
r=113
|CD|=30
|AB|=178
|CD|=30
|AB|=178
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20783 ⋅ Poprawnie: 54/91 [59%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
Z punktu C leżącego poza okręgiem poprowadzono
sieczną okręgu zawierającą środek okręgu S oraz
taką sieczną przecinającą ten okrąg w punktach A
i B, że |SB|=|BC|.
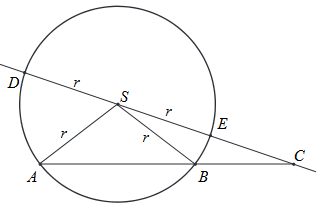

Oblicz |\sphericalangle ASD|.
Dane
|\sphericalangle BCE|=16^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 2 pkt ⋅ Numer: pp-20894 ⋅ Poprawnie: 86/175 [49%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
» Punkt O jest środkiem okręgu:
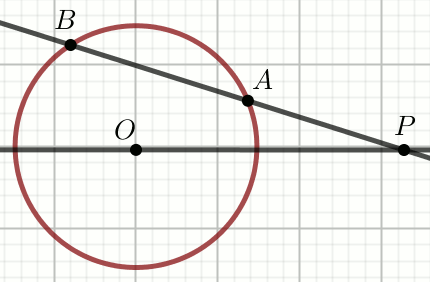

Oblicz długość promienia tego okręgu.
Dane
|AP|=16
|AB|=12
|OP|=23
|AB|=12
|OP|=23
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 4 pkt ⋅ Numer: pp-30395 ⋅ Poprawnie: 68/153 [44%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
«« Punkt O jest środkiem okręgu:


Oblicz |AC|.
Dane
|AB|=17
|BN|=8
|CN|=4
|BN|=8
|CN|=4
Odpowiedź:
|AC|=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 8.2 (2 pkt)
Oblicz |MC|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)