⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-13-okr-i-kola-pr-1
| Zadanie 1. 1 pkt ⋅ Numer: pp-10506 ⋅ Poprawnie: 216/282 [76%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Punkt O jest środkiem a prosta jest styczną
to tego okręgu, przy czym
\alpha=82^{\circ}:
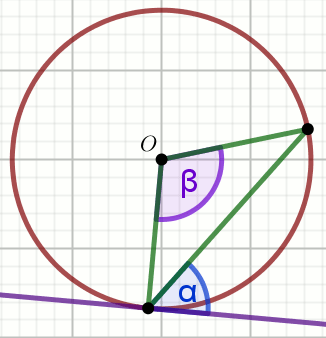
Wyznacz miarę stopniową kąta \beta.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10545 ⋅ Poprawnie: 81/112 [72%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Punkt O jest środkiem okręgu, a prosta
k styczną do tego okręgu w punkcie
A:
.
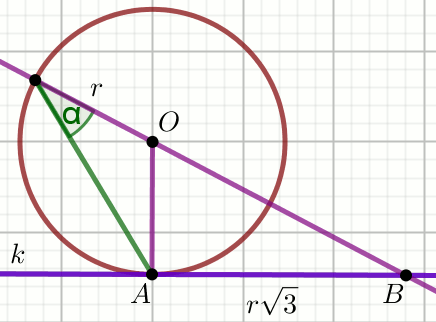
Wyznacz miarę stopniową kąta \alpha.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 1 pkt ⋅ Numer: pp-11655 ⋅ Poprawnie: 25/43 [58%] | Rozwiąż |
Podpunkt 3.1 (0.5 pkt)
Okręgi o_1(A, r_1) oraz o_2(B,r_2)
(r_1\lessdot r_2) są styczne wewnętrznie, a odległość ich środków jest równa \frac{5}{2}.
Suma długości promieni tych okręgów jest równa \frac{9}{2}.
Oblicz r_1.
Odpowiedź:
| r_1= | |
Podpunkt 3.2 (0.5 pkt)
Oblicz r_2.
Odpowiedź:
| r_2= | |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11648 ⋅ Poprawnie: 90/142 [63%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Odcinek AB ma długość 48
i jest cięciwą okręgu o promieniu \frac{73}{2}.
Oblicz odległość d cięciwy AB od środka tego okręgu.
Odpowiedź:
| d= | |
| Zadanie 5. 2 pkt ⋅ Numer: pp-20226 ⋅ Poprawnie: 43/93 [46%] | Rozwiąż |
Podpunkt 5.1 (2 pkt)
W okręgu o środku O i promieniu długości
r poprowadzono dwie równoległe cięciwy
AB i CD położone
po tej samej stronie środka okręgu:
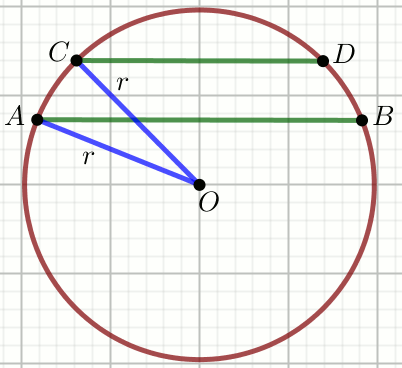
Oblicz odległość pomiędzy tymi cięciwami.
Dane
r=37
|CD|=24
|AB|=48
|CD|=24
|AB|=48
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. 2 pkt ⋅ Numer: pp-20229 ⋅ Poprawnie: 135/246 [54%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
» Do dwóch stycznych zewnętrznie okręgów o promieniach
r_1 i r_2
i środkach odpowiednio O_1 i
O_2, poprowadzono styczną, która przecięłą
prostą przechodzącą przez środki tych okręgów w punkcie
A:
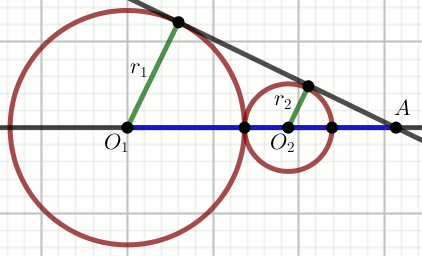
Oblicz długość odcinka O_1A.
Dane
r_1=27
r_2=26
r_2=26
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 4 pkt ⋅ Numer: pp-30018 ⋅ Poprawnie: 37/93 [39%] | Rozwiąż |
Podpunkt 7.1 (4 pkt)
» Znając długość odcinka AB na rysunku
oblicz iloczyn promieni tych kół:
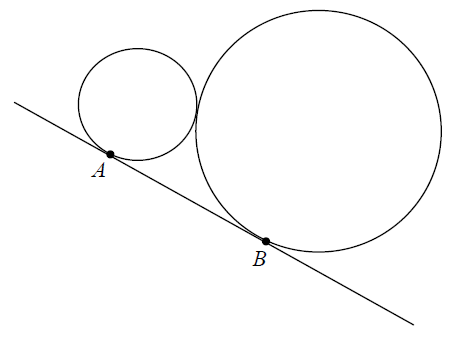
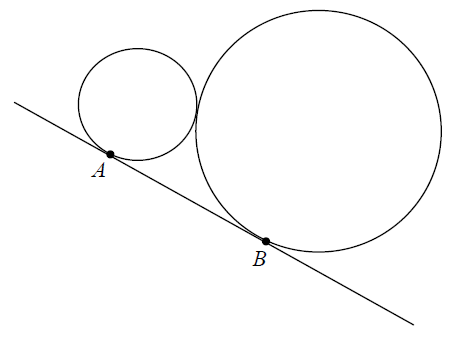
Dane
|AB|=14
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)