Podgląd testu : lo2@sp-16-trojkaty-pole-pp-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-10515 ⋅ Poprawnie: 92/170 [54%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku
25:36, mogą być równe:
Odpowiedzi:
| A. 5:\frac{36}{5} | B. 10:\frac{25}{2} |
| C. 18:10 | D. 5:\frac{25}{6} |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11601 ⋅ Poprawnie: 9/11 [81%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Stosunek pola powierzchni trójkąta do pola powierzchni koła wpisanego w ten trójkąt jest równy
8:\pi, a średnica tego koła ma długość 8.
Oblicz długość obwodu tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10647 ⋅ Poprawnie: 380/532 [71%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
W trójkącie równoramiennym ramię o długości
7\sqrt{2} tworzy z podstawą kąt o mierze
67,5^{\circ}.
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 4. 1 pkt ⋅ Numer: pp-10656 ⋅ Poprawnie: 354/511 [69%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Przekątne równoległoboku mają długość
4 i 16,
a kąt między tymi przekątnymi ma miarę
30^{\circ}.
Oblicz pole powierzchni tego równoległoboku.
Odpowiedź:
| P= | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10679 ⋅ Poprawnie: 172/233 [73%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Pole powierzchni rombu o obwodzie długości 56 jest równe
49. Kąt ostry tego rombu ma miarę
\alpha.
Wówczas:
Odpowiedzi:
| A. 60^{\circ} \lessdot \alpha \lessdot 61^{\circ} | B. 29^{\circ} \lessdot \alpha \lessdot 30^{\circ} |
| C. 14^{\circ} \lessdot \alpha \lessdot 15^{\circ} | D. 75^{\circ} \lessdot \alpha \lessdot 76^{\circ} |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20901 ⋅ Poprawnie: 14/19 [73%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
« Pole powierzchni trójkąta prostokątnego jest równe 240,
a tangens jednego z kątów ostrych tego trójkąta jest równy \frac{15}{8}.
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
| R= | |
| Zadanie 7. 2 pkt ⋅ Numer: pp-21027 ⋅ Poprawnie: 38/65 [58%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
« Pole powierzchni trójkąta równoramiennego jest równe 672, a tangens kąta
kąta przy podstawie jest równy \frac{24}{7}.
Oblicz długość obwodu tego trójkąta.
Odpowiedź:
L=
(wpisz liczbę całkowitą)
Podpunkt 7.2 (1 pkt)
Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
| r= | |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20756 ⋅ Poprawnie: 57/207 [27%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
« Dane są punkty na okręgu:
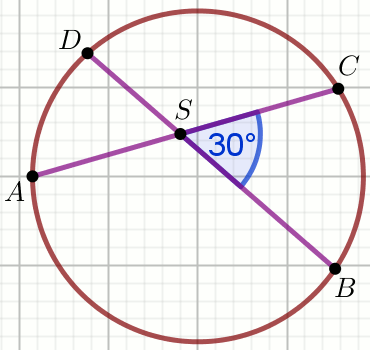

Oblicz P_{\triangle ASD}.
Dane
|AS|=13
|SB|=7
|SC|=17
|SB|=7
|SC|=17
Odpowiedź:
| P_{\triangle ASD}= | |
| Zadanie 9. 2 pkt ⋅ Numer: pp-20765 ⋅ Poprawnie: 47/195 [24%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
« Punkt O jest środkiem okręgu. Oblicz pole
powierzchni niebieskiego obszaru:
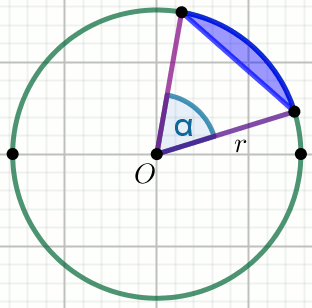

Dane
r=6
\alpha=45^{\circ}
\alpha=45^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)