Podgląd testu : lo2@sp-16-trojkaty-pole-pp-3
| Zadanie 1. 1 pkt ⋅ Numer: pp-10515 ⋅ Poprawnie: 92/170 [54%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku
49:64, mogą być równe:
Odpowiedzi:
| A. 24:14 | B. 14:\frac{147}{8} |
| C. 7:\frac{49}{8} | D. 8:\frac{49}{8} |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11602 ⋅ Poprawnie: 5/11 [45%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
W trójkącie prostokątnym stosunek długości przyprostokątnej do długości przeciwprostokątnej jest równy
33:65.
Oblicz stosunek pola powierzchni koła wpisanego w ten trójkąt do pola powierzchni koła opisanego na tym trójkącie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10678 ⋅ Poprawnie: 417/518 [80%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
» Oblicz pole powierzchni rombu o boku długości 14 i kącie rozwartym
120^{\circ}.
Odpowiedź:
| P= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 4. 1 pkt ⋅ Numer: pp-10666 ⋅ Poprawnie: 259/456 [56%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« Przyprostokątna trójkąta o długości 4 jest jednym
z ramion kąta ostrego tego trójkąta o mierze 30^{\circ}
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 5. 1 pkt ⋅ Numer: pp-10667 ⋅ Poprawnie: 258/335 [77%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Każde z ramion trójkąta równoramiennego ma długość 18.
Kąt zawarty między ramionami tego trójkąta ma miarę
150^{\circ}.
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 6. 2 pkt ⋅ Numer: pp-20745 ⋅ Poprawnie: 43/196 [21%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
» Odcinki AM i MB
na rysunku maja równą długość, a bok AC ma długość
14:
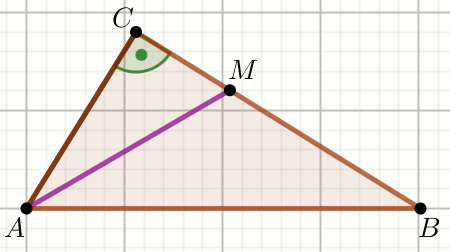

Wiedząc, że P_{\triangle ABC}=98\sqrt{3}, oblicz P_{\triangle ABM}.
Odpowiedź:
| P_{\triangle ABM}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 7. 2 pkt ⋅ Numer: pp-20908 ⋅ Poprawnie: 38/71 [53%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
W trójkącie równoramiennym podstawa ma długość 112, a cosinus
kąta przy podstawie jest równy \frac{56}{65}.
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
P_{\triangle}=
(wpisz liczbę całkowitą)
Podpunkt 7.2 (1 pkt)
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
| R= | |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20757 ⋅ Poprawnie: 16/88 [18%] | Rozwiąż |
Podpunkt 8.1 (1 pkt)
» Dany jest trójkąt równoramienny o podstawie
AB:
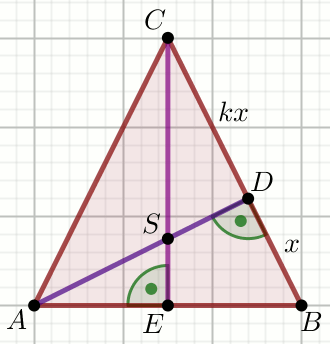

Oblicz \sin\sphericalangle DAB.
Dane
k=4
Odpowiedź:
| \sin\sphericalangle DAB= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 8.2 (1 pkt)
Oblicz
\frac{P_{\triangle AES}}{P_{\triangle SDC}}
.
Odpowiedź:
| \frac{P_{\triangle AES}}{P_{\triangle SDC}}= | |
| Zadanie 9. 2 pkt ⋅ Numer: pp-20761 ⋅ Poprawnie: 65/213 [30%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
» Łuk \stackrel{\frown}{\ AB\ } ma długość
l:
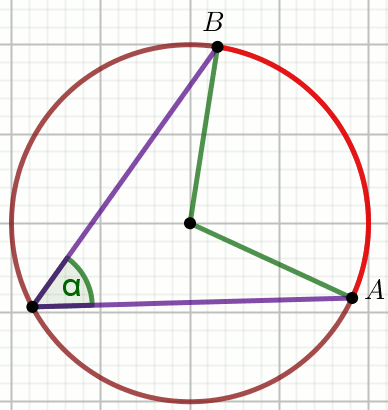

Oblicz pole powierzchni wycinka kołowego wyznaczonego przez ten łuk.
Dane
l=6\pi=18.84955592153876
\alpha=36^{\circ}
\alpha=36^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. 2 pkt ⋅ Numer: pp-20890 ⋅ Poprawnie: 211/342 [61%] | Rozwiąż |
Podpunkt 10.1 (2 pkt)
« Dany jest trójkąt, w którym:
\sin\alpha=\frac{2}{3},
\cos\beta=\frac{1}{2} i
|BC|=8:
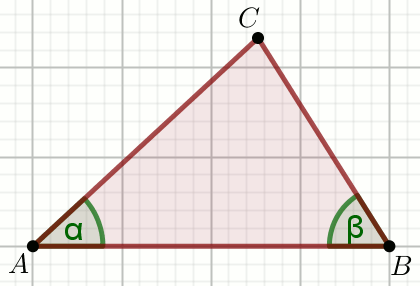

Oblicz |AC|.
Odpowiedź:
| |AC|= | ||
| (wpisz trzy liczby całkowite) | ||