Podgląd testu : lo2@sp-16-trojkaty-pole-pr-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-10587 ⋅ Poprawnie: 430/615 [69%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Trójkąty ABC i
A'B'C' są podobne, a ich pola powierzchni są odpowiednio,
równe 2 cm2 i
90 cm2.
Wyznacz skalę tego podobieństwa \frac{|A'B'|}{|AB|}.
Odpowiedź:
| \frac{|A'B'|}{|AB|}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 2. 1 pkt ⋅ Numer: pp-11600 ⋅ Poprawnie: 68/105 [64%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Punkt O jest środkiem koła na rysunku, a promień r tego
koła ma długość 18. Kąt środkowy koła \alpha
oparty jest na łuku o długości 1\pi:
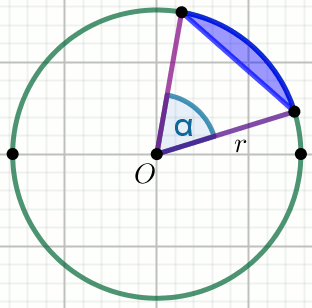

Oblicz pole powierzchni zaznaczonego na rysunku odcinka koła.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 1 pkt ⋅ Numer: pp-10647 ⋅ Poprawnie: 380/532 [71%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
W trójkącie równoramiennym ramię o długości
4 tworzy z podstawą kąt o mierze
67,5^{\circ}.
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 4. 1 pkt ⋅ Numer: pp-10673 ⋅ Poprawnie: 235/366 [64%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
» Przekątne równoległoboku o długości 13
i \frac{7}{2} przecinają się pod kątem rozwartym o mierze
150^{\circ}.
Oblicz pole powierzchni tego równoległoboku.
Odpowiedź:
| P= | |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11512 ⋅ Poprawnie: 483/859 [56%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Oblicz pole powierzchni prostokąta,którego przekątne mają długość 32 i
przecinają się pod kątem o mierze 60^{\circ}.
Odpowiedź:
| P= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 6. 2 pkt ⋅ Numer: pr-20567 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 6.1 (2 pkt)
Dany jest trójkąt ABC, w którym:
|AC|=11,
|BC|=22 oraz
P_{\triangle DBC}-P_{\triangle ADC}=\frac{121\sqrt{3}}{6}:
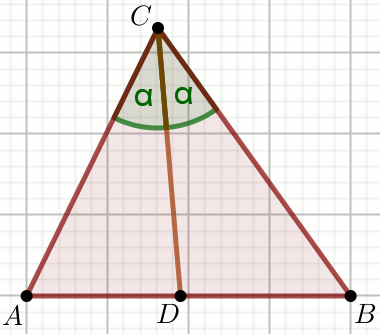

Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
| P_{\triangle ABC}= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 7. 2 pkt ⋅ Numer: pp-21026 ⋅ Poprawnie: 2/92 [2%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Pole powierzchni trójkąta równoramiennego jest równe 3072, a cosinus
kąta przy podstawie jest równy \frac{3}{5}.
Oblicz długość obwodu tego trójkąta.
Odpowiedź:
L=
(wpisz liczbę całkowitą)
Podpunkt 7.2 (1 pkt)
Oblicz długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
| r= | |
| Zadanie 8. 2 pkt ⋅ Numer: pp-20912 ⋅ Poprawnie: 21/34 [61%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
W trójkącie ostrokątnym równoramiennym ABC, |AC|=|BC|,
poprowadzono wysokości CD i BE. Stosunek pól powierzchni
trójkątów ABE i ADC jest równy
P_{ABE}:P_{ADC}=\frac{36}{25}, a obwód tego trójkąta ma długość
32.
Oblicz pole powierzchni trójkąta ABC.
Odpowiedź:
P_{\triangle ABC}=
(wpisz liczbę całkowitą)
| Zadanie 9. 2 pkt ⋅ Numer: pp-20766 ⋅ Poprawnie: 77/170 [45%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
W wycinek kołowy o kącie środkowym \alpha
wpisano okrąg o polu powierzchni P:
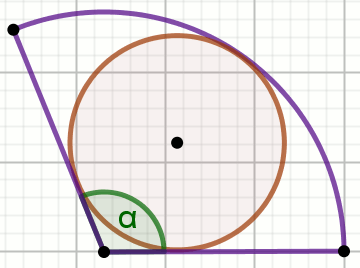

Oblicz pole powierzchni tego wycinka.
Dane
\alpha=120^{\circ}
P=16\pi=50.26548245743669
P=16\pi=50.26548245743669
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. 2 pkt ⋅ Numer: pp-20886 ⋅ Poprawnie: 128/201 [63%] | Rozwiąż |
Podpunkt 10.1 (2 pkt)
» Oblicz długość niebieskiego odcinka na rysunku wiedząc, że:
|AD|=100,
|DB|=2,
|AC|=125,
|BC|=\sqrt{5629}:
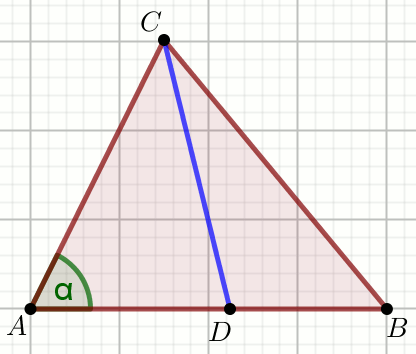

Odpowiedź:
|CD|=
(wpisz liczbę całkowitą)
| Zadanie 11. 4 pkt ⋅ Numer: pr-30380 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 11.1 (4 pkt)
« W trójkącie na rysunku dane są długości odcinków:
|AD|=1,
|DB|=\frac{5}{2},
|BC|=2\sqrt{2} i
|AC|=\frac{5}{2}:
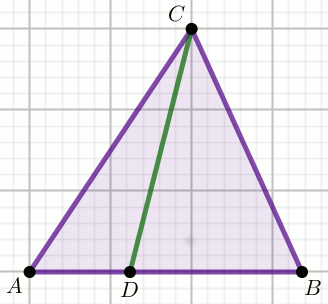

Oblicz \sin\sphericalangle{ADC}.
Odpowiedź:
\sin\sphericalangle{ADC}=
(liczba zapisana dziesiętnie)