⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-analiza-pr-2
| Zadanie 1. 1 pkt ⋅ Numer: pr-10340 ⋅ Poprawnie: 3/3 [100%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Oblicz granicę
\lim_{x\to 6^{-}} \frac{x-4}{(x-6)(-2-x)}
.
Jako odpowiedź wpisz:
- 999, jeżeli granica jest równa +\infty,
- -999, jeżeli granica jest równa -\infty,
- obliczoną granicę w każdym innym przypadku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. 1 pkt ⋅ Numer: pr-10351 ⋅ Poprawnie: 3/3 [100%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Oblicz granicę
\lim_{x\to {x_0}^+} \frac{ax+b}{x^2+cx+d}
.
Jako odpowiedź wpisz:
- 999, jeżeli granica jest równa +\infty,
- -999, jeżeli granica jest równa -\infty,
- obliczoną granicę w każdym innym przypadku.
Dane
x_0=-2
a=-2
b=4
c=-5
d=-14
a=-2
b=4
c=-5
d=-14
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 1 pkt ⋅ Numer: pr-10355 ⋅ Poprawnie: 20/22 [90%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
» Funkcja określona wzorem
f(x)=\left\lbrace
\begin{array}{ll}
\frac{x^2+8x+15}{x+5} & \text{dla }x\neq -5\\
m & \text{dla }x=-5
\end{array}
jest funkcją ciągłą w swojej dziedzinie.
Wyznacz wartość parametru m.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. 2 pkt ⋅ Numer: pr-20845 ⋅ Poprawnie: 27/27 [100%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
» Dana jest funkcja
f(x)=
\begin{cases}
\frac{x^2+a}{x-2} \text{, dla } x\neq 2 \\
b\text{, dla } x=2
\end{cases}
,
która jest ciągła w punkcie x=2.
Podaj a.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 4.2 (1 pkt)
Podaj b.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. 2 pkt ⋅ Numer: pr-20849 ⋅ Poprawnie: 19/22 [86%] | Rozwiąż |
Podpunkt 5.1 (1.6 pkt)
« Rozwiąż równanie f(x)=f'(x), gdzie
f(x)=\frac{x-5}{x-9}.
Podaj największe z rozwiązań całkowitych tego równania.
Odpowiedź:
x=
(liczba zapisana dziesiętnie)
Podpunkt 5.2 (0.4 pkt)
Ile rozwiązań ma to równanie?
Odpowiedź:
ile=
(wpisz liczbę całkowitą)
| Zadanie 6. 2 pkt ⋅ Numer: pr-20861 ⋅ Poprawnie: 1/21 [4%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
« Wyznacz równanie stycznej do wykresu funkcji
f(x)=\frac{5x+2}{x+6}-3 w punkcie
x_0=4 i zapisz je w postaci
y=ax+b.
Podaj a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 6.2 (1 pkt)
Podaj b.
Odpowiedź:
b=
(wpisz liczbę całkowitą)
| Zadanie 7. 2 pkt ⋅ Numer: pr-20863 ⋅ Poprawnie: 40/36 [111%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
Wyznacz przedziały monotoniczności funkcji
f(x)=x+\frac{9}{x}.
Podaj sumę prawych końców tych wszystkich przedziałów, w których funkcja ta jest malejąca.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 4 pkt ⋅ Numer: pr-30811 ⋅ Poprawnie: 8/8 [100%] | Rozwiąż |
Podpunkt 8.1 (2 pkt)
Dana jest funkcja g(m)=x_1\cdot x_2, gdzie
x_1 i x_2 są różnymi
pierwiastkami równania (m-1)x^2+(m-2)x+m^2-4m+4=0.
Wyznacz te wartości parametru m, dla których funkcja
g osiąga maksimum lokalne.
Podaj najmniejsze możliwe m spełniające warunki zadania.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.2 (2 pkt)
Ile wynosi to maksimum?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. 6 pkt ⋅ Numer: pr-30359 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 9.1 (4 pkt)
» Największy z okręgów na rysunku ma promień długości
36, a punkty O,
O_1 i O_2 nie
leżą na jednej prostej:
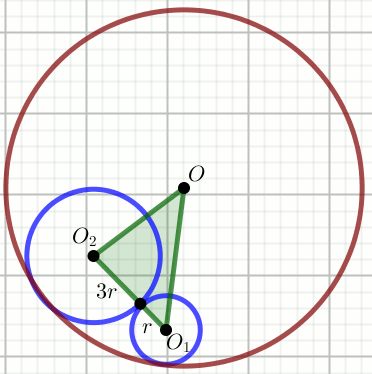
Wyraź pole powierzchni zielonego trójkąta jako funkcję promienia r (wykorzystaj wzór P=\sqrt{p(p-a)(p-b)(p-c)}).
Wyznacz długość promienia r, przy której pole zielonego trójkąta jest największe.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.2 (2 pkt)
Ile jest równe to największe pole?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)