⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@sp-fun-wyk-log-pr-1
| Zadanie 1. 1 pkt ⋅ Numer: pr-10165 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 1.1 (0.2 pkt)
Dziedziną funkcji określonej wzorem
g(x)=\frac{3\sqrt{3}}{\sqrt{\left(\frac{1}{a}\right)^x-b}}
jest zbiór postaci:
Dane
a=5
b=625
b=625
Odpowiedzi:
| A. (-\infty, p) | B. (p, q) |
| C. (-\infty, p\rangle | D. \langle p, q\rangle |
| E. (p,+\infty) | F. \langle p,+\infty) |
Podpunkt 1.2 (0.8 pkt)
Zapisz tę dziedzinę w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych
tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. 1 pkt ⋅ Numer: pp-11194 ⋅ Poprawnie: 53/114 [46%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Wykres funkcji y=-2-\frac{1}{10^x} nie przecina
prostej:
Odpowiedzi:
| A. y=-2-\sqrt{2} | B. x=\sqrt{5} |
| C. y=-2+\sqrt{2} | D. y=10x |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11213 ⋅ Poprawnie: 491/627 [78%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Wykres funkcji f(x)=2^{x-3} przedstawia rysunek:
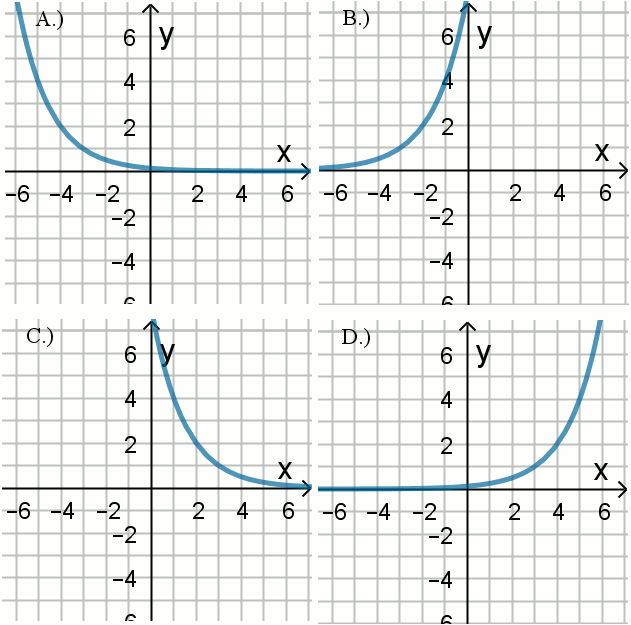
Odpowiedzi:
| A. C | B. D |
| C. A | D. B |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11202 ⋅ Poprawnie: 303/402 [75%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Do wykresu funkcji określonej wzorem f(x)=3^x+m należy punkt
o współrzędnych P=(6,-30).
Wyznacz wartość parametru m.
Odpowiedź:
| m= | |
| Zadanie 5. 1 pkt ⋅ Numer: pr-10153 ⋅ Poprawnie: 0/1 [0%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Wyznacz dziedzinę funkcji określonej wzorem f(x)=\log_{x}{(ax-1)}.
Rozwiązanie zapisz w postaci sumy przedziałów.
Podaj najmniejszy i największy z końców liczbowych tych przedziałów.
Dane
a=8
Odpowiedzi:
| x_{min} | = |
(wpisz liczbę zapisaną dziesiętnie) |
| x_{max} | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20574 ⋅ Poprawnie: 104/159 [65%] | Rozwiąż |
Podpunkt 6.1 (2 pkt)
Rozwiąż równanie:
3^x\cdot \left(\frac{1}{3}\right)^{x-a}=\left(\frac{1}{27}\right)^{x}
Podaj rozwiązanie tego równania.
Dane
a=15
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. 2 pkt ⋅ Numer: pp-20551 ⋅ Poprawnie: 16/33 [48%] | Rozwiąż |
Podpunkt 7.1 (2 pkt)
« Rozwiąż nierówność:
3^{3x+3a+1}-4\cdot 27^{x+a-1}+9^{\frac{3}{2}(x+a)-1} \lessdot 80
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Dane
a=12
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 4 pkt ⋅ Numer: pr-30238 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 8.1 (1 pkt)
« Naszkicuj wykres funkcji f(x)=\left|a^{x+1}-b\right|.
Podaj największą wartość tej funkcji w przedziale \langle -1,2\rangle.
Dane
a=10
b=11
b=11
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.2 (1 pkt)
Podaj najmniejszą wartość tej funkcji w przedziale
\langle -1,2\rangle.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.3 (2 pkt)
Dla jakich wartości parametru m równanie
f(x)=m ma dwa rozwiązania?
Rozwiązanie zapisz w postaci przedziału. Podaj prawy koniec tego przedziału.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. 4 pkt ⋅ Numer: pp-30176 ⋅ Poprawnie: 8/37 [21%] | Rozwiąż |
Podpunkt 9.1 (4 pkt)
« Rozwiąż nierówność
a^{1+6+11+...+(5x-4)} \leqslant b^c
.
Podaj największą liczbę całkowitą spełniającą tę nierówność.
Dane
a=10
b=1000
c=9
b=1000
c=9
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)