Podgląd testu : lo2@sp-fun-wyk-pp-2
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11211 |
Podpunkt 1.1 (1 pkt)
Wskaż argument, dla którego funkcja określona wzorem
f(x)=(\sqrt{a})^x
przyjmuje wartość b:
Dane
a=5
b=9
b=9
Odpowiedzi:
| A. \log_{5}{9} | B. 9\cdot \log_{5}{81} |
| C. \log_{5}{81} | D. \frac{\log_{5}{9}}{2} |
| E. \log_{9}{9} | F. \log_{9}{25} |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11200 |
Podpunkt 2.1 (1 pkt)
Dana jest funkcja f(x)=a^x. Punkt
A=(p, q) należy do wykresu tej funkcji.
Podaj liczbę a.
Dane
p=4
q=1296
q=1296
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11191 |
Podpunkt 3.1 (1 pkt)
» Dana jest funkcja g(x)=(\sqrt{a})^x.
Zbiór ZW_g nie zawiera liczby:
Dane
a=7
Odpowiedzi:
| A. \frac{\sqrt{\pi}}{6} | B. 5^{-7} |
| C. 12\cdot \pi -38 | D. 17\cdot \pi -53 |
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11194 |
Podpunkt 4.1 (1 pkt)
Wykres funkcji y=b-\frac{1}{a^x} nie przecina
prostej:
Dane
a=8
b=1
b=1
Odpowiedzi:
| A. x=\sqrt{17} | B. y=1+\sqrt{2} |
| C. y=1-\sqrt{2} | D. y=8x |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11201 |
Podpunkt 5.1 (1 pkt)
Funkcja g(x)=4^{ax+1} przyjmuje wartość:
Dane
a=4
Odpowiedzi:
| A. -\frac{1}{7} | B. -\frac{\pi}{2} |
| C. \frac{\sqrt{7}}{7} | D. 0 |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11189 |
Podpunkt 6.1 (1 pkt)
Zbiór wartości funkcji f(x)=a^x+\sqrt{b}
zawiera liczbę:
Dane
a=5
b=20
b=20
Odpowiedzi:
| A. \frac{\sqrt{20}}{5} | B. \sqrt{20}+3 |
| C. -22 | D. \sqrt{20}-4 |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11206 |
Podpunkt 7.1 (1 pkt)
» Wykres funkcji f(x)=\frac{1}{b}\cdot a^x otrzymamy
przesuwając wykres funkcji g(x)=a^x o:
Dane
a=4
b=256
b=256
Odpowiedzi:
| A. dwie jednostki w górę | B. cztery jednostki w lewo |
| C. cztery jednostki w dół | D. cztery jednostki w prawo |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11213 |
Podpunkt 8.1 (1 pkt)
« Wykres funkcji f(x)=2^{x-3} przedstawia rysunek:
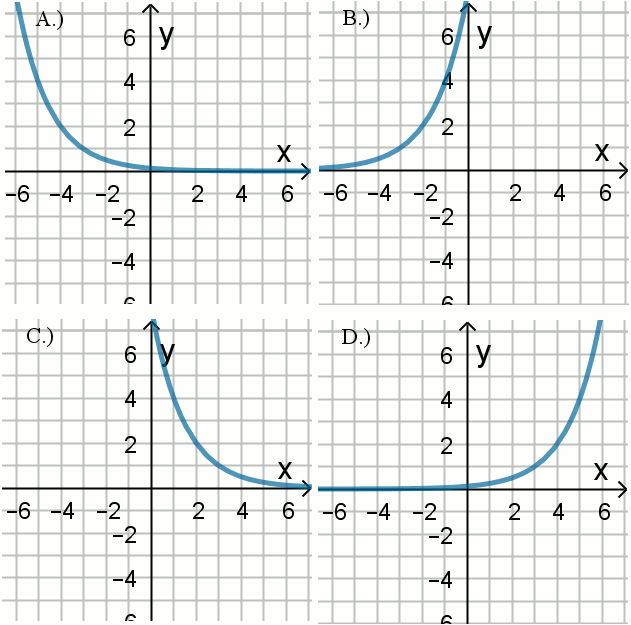

Odpowiedzi:
| A. B | B. C |
| C. D | D. A |
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11202 |
Podpunkt 9.1 (1 pkt)
Do wykresu funkcji określonej wzorem f(x)=3^x+m należy punkt
o współrzędnych P=(a,b).
Wyznacz wartość parametru m.
Dane
a=4
b=-11
b=-11
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11209 |
Podpunkt 10.1 (1 pkt)
Podaj wspólne rozwiązanie równań
a^{x^2}\cdot \sqrt{a}=a^{\frac{b}{2}}
oraz \log_{\frac{1}{a}}{x}=-1.
Dane
a=7
b=99
b=99
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)