Podgląd testu : lo2@sp-geom-analit-pr-2
| Zadanie 1. 1 pkt ⋅ Numer: pp-11230 ⋅ Poprawnie: 183/268 [68%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Zapisz długość okręgu o środku w punkcie S=(-6,-5), do którego
należy punkt o współrzędnych A=(-2,1) w postaci
p\cdot\pi.
Podaj liczbę p.
Odpowiedź:
p=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
| Zadanie 2. 1 pkt ⋅ Numer: pp-11241 ⋅ Poprawnie: 273/431 [63%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Punkt S=\left(\frac{25}{4},-6\right) jest środkiem odcinka
AB, gdzie A=(x_A,y_A) i
B=(-5,-2).
Podaj współrzedne x_A i y_A.
Odpowiedzi:
| x_A | = | (dwie liczby całkowite) | |
| y_A | = | (dwie liczby całkowite) | |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11231 ⋅ Poprawnie: 201/333 [60%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Środek odcinka o końcach (5,-5) i
(7,-5) należy do prostej o równaniu
y+ax=-1+4a.
Wyznacz wartość parametru a.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
| Zadanie 4. 1 pkt ⋅ Numer: pr-10225 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Oblicz odległość punktu o współrzędnych (-1,0) od prostej
o równaniu 2x-y-3=0.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. 1 pkt ⋅ Numer: pr-10208 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Dana jest prosta 3x-4y-5=0. Który z okręgów jest
styczny do tej prostej:
Odpowiedzi:
| A. (x-4)^2+(y+2)^2=9 | B. (x-3)^2+(y+2)^2=3 |
| C. (x-3)^2+(y+3)^2=9 | D. (x-3)^2+(y+3)^2=3 |
| Zadanie 6. 2 pkt ⋅ Numer: pr-20357 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 6.1 (1 pkt)
» Prosta o równaniu
2x-(2m-15)y+2m-7=0 przecina prostą
(2m-15)x+y-m+\frac{13}{2}=0 w punkcie
P=(0, y_0).
Podaj najmniejsze możliwe m.
Odpowiedź:
| m_{min}= | |
Podpunkt 6.2 (1 pkt)
Podaj największe możliwe m.
Odpowiedź:
| m_{max}= | |
| Zadanie 7. 2 pkt ⋅ Numer: pp-20624 ⋅ Poprawnie: 14/67 [20%] | Rozwiąż |
Podpunkt 7.1 (1 pkt)
Prosta k przechodząca przez punkt C=(12,16)
przecina osie układu współrzędnych w punktach A i
B=(x_b,y_b) i jest prostopadła o odcinka OC:
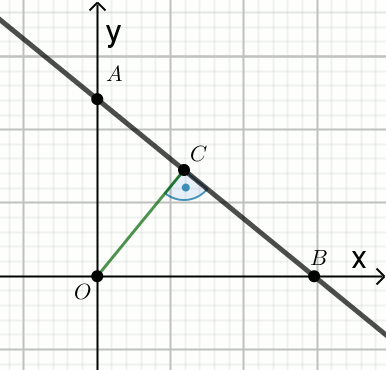

Podaj x_b.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 7.2 (1 pkt)
Oblicz |AB|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. 2 pkt ⋅ Numer: pr-20409 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 8.1 (1 pkt)
Obrazem prostej y=ax+b w jednokładności
J^k_{S=(x_s,y_s)} jest prosta
y=a_1x+b_1.
Podaj a_1.
Dane
a=2
b=-13
x_s=4
y_s=-2
k=-\frac{1}{3}=-0.333333333333333
b=-13
x_s=4
y_s=-2
k=-\frac{1}{3}=-0.333333333333333
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 8.2 (1 pkt)
Punkt S=(x_s,y_s) jest środkiem tej jednokładności
w skali ujemnej.
Podaj x_s.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. 4 pkt ⋅ Numer: pp-30193 ⋅ Poprawnie: 28/61 [45%] | Rozwiąż |
Podpunkt 9.1 (2 pkt)
Trójkąt ABC ma wierzchołki:
A=(x_a,y_a), B=(x_b,y_b) i
C=(x_c,y_c).
Wyznacz długość najkrótszej wysokości tego trójkąta.
Dane
x_a=1
y_a=2
x_b=1
y_b=1
x_c=5
y_c=-1
y_a=2
x_b=1
y_b=1
x_c=5
y_c=-1
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.2 (2 pkt)
Wyznacz długość najdłuższej wysokości tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. 4 pkt ⋅ Numer: pp-30238 ⋅ Poprawnie: 0/5 [0%] | Rozwiąż |
Podpunkt 10.1 (2 pkt)
Dane są punkty A=(9,-4),
B=(3,2) i C=(0,-7),
które są wierzchołkami trójkąta, a prosta o równaniu x+by+c=0 jest osią symetrii tego trójkąta.
Podaj c.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 10.2 (2 pkt)
Oblicz pole powierzchni tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. 4 pkt ⋅ Numer: pr-30312 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 11.1 (1 pkt)
Dane sa okręgi o_1:x^2+y^2+a_1x+b_1y+c_1=0 oraz
o_2:x^2+y^2+a_2x+b_2y+c_2=0. Wiadomo, że
J^{k}_{S}(o_1)=o_2. Wyznacz środek
S=(x_s,y_s) i skalę k
tej jednokładności.
Podaj ujemną skalę k.
Dane
a_1=-16
b_1=18
c_1=120
a_2=-64
b_2=36
c_2=948
b_1=18
c_1=120
a_2=-64
b_2=36
c_2=948
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.2 (1 pkt)
Podaj x_s wyznaczone dla skali dodatniej.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.3 (1 pkt)
Podaj y_s wyznaczone dla skali dodatniej.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 11.4 (1 pkt)
Podaj x_s wyznaczone dla skali ujemnej.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)