⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-04-02-wykres-funkcji-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-10701 ⋅ Poprawnie: 198/473 [41%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
» Na rysunku przedstawiony jest fragment wykresu funkcji liniowej
f, przy czym
f(0)=-2 i f(1)=0.
Wykres funkcji g jest symetryczny do wykresu funkcji f względem początku układu współrzędnych.
Funkcja g jest określona wzorem:
Odpowiedzi:
| A. g(x)=2x-2 | B. g(x)=-2x+2 |
| C. g(x)=2x+2 | D. g(x)=-2x-2 |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10723 ⋅ Poprawnie: 205/343 [59%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Do wykresu funkcji f(x)=(m-1)x+m^2-20 należy punkt
P=(0,5).
Wyznacz wartość parametru m wiedząc, że jest ona dodatnia.
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10731 ⋅ Poprawnie: 403/922 [43%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Na rysunku przedstawiono wykres funkcji
y=f(x).
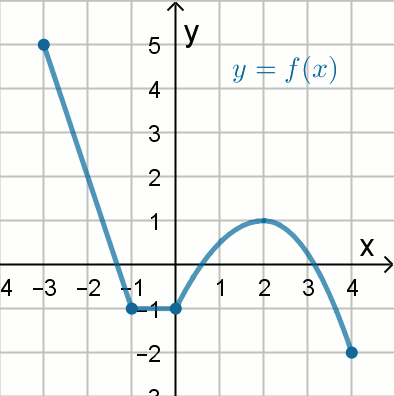
W którym z przedziałów, funkcja przyjmuje wartość 1:
Odpowiedzi:
| A. \langle 2,4) | B. (2,3) |
| C. (-1,2) | D. \langle 1,2) |
| Zadanie 4. 2 pkt ⋅ Numer: pp-20293 ⋅ Poprawnie: 123/224 [54%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
» Dla jakich wartości parametru m\in\mathbb{R} wykresy funkcji
f(x)=\frac{2x+m}{x-5} oraz
g(x)=-4^{x-1} przecinają oś
Oy w tym samym punkcie.
Podaj najmniejszą możliwą wartość parametru m.
Odpowiedź:
| m_{min}= | |