Podgląd testu : lo2@zd-04-04-zbior-wartosci-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-10721 ⋅ Poprawnie: 219/402 [54%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Wykres funkcji f pokazano na rysunku:
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : \frac{1}{f(1)} > f(4) | T/N : \left[f(-4)\right]^2 < f(4) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10714 ⋅ Poprawnie: 295/395 [74%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Funkcja f każdej liczbie naturalnej ze zbioru
\{
10,16,19,24\} przyporządkowuje resztę z dzielenia
tej liczby przez 4.
Zbiorem wartości tej funkcji jest zbiór:
Odpowiedzi:
| A. \{0,1,3\} | B. \{0,2,3\} |
| C. \{0,1,2\} | D. \{1,2,3\} |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10727 ⋅ Poprawnie: 508/752 [67%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Na rysunku przedstawiono wykres funkcji
f:
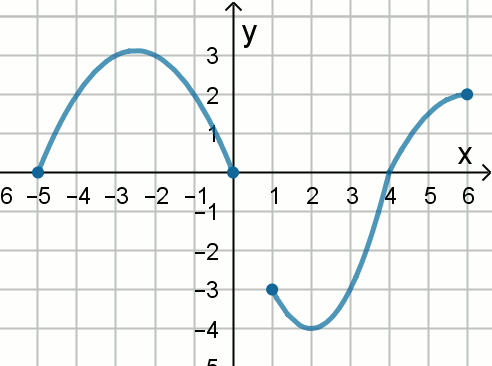
Zbiorem wartości funkcji g określonej wzorem g(x)=f(x)-3 jest zbiór:
Odpowiedzi:
| A. \left\langle -6,\frac{9}{8}\right\rangle | B. \left\langle -7,\frac{1}{8}\right\rangle |
| C. \left\langle -9,-\frac{15}{8}\right\rangle | D. \left\langle -5,\frac{17}{8}\right\rangle |
| Zadanie 4. 1 pkt ⋅ Numer: pp-10753 ⋅ Poprawnie: 58/83 [69%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Wartością funkcji dla argumentu naturalnego n jest
ostatnia cyfra kwadratu liczby n zwiększona o
2. Wynika stąd, że zbiór wartości funkcji zawiera
liczbę:
Odpowiedzi:
| A. 9 | B. 4 |
| C. 5 | D. 7 |
| Zadanie 5. 1 pkt ⋅ Numer: pp-10763 ⋅ Poprawnie: 118/164 [71%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Do wykresu funkcji f(x)=ax+\frac{1}{4} określonej dla
x\neq -1 należy punkt
A=(-2,3).
Wyznacz wartość parametru a.
Odpowiedź:
| \frac{m}{n}= | |
| Zadanie 6. 2 pkt ⋅ Numer: pp-20773 ⋅ Poprawnie: 93/227 [40%] | Rozwiąż |
Podpunkt 6.1 (1 pkt)
« Dana jest funkcja f(x)=\frac{1}{x},
gdzie x\in\left(-2, -\frac{3}{16}\right).
Podaj najmniejszą liczbę całkowitą, która należy do zbioru wartości tej funkcji.
Odpowiedź:
min_{\in\mathbb{Z},\in ZW_f}=
(wpisz liczbę całkowitą)
Podpunkt 6.2 (1 pkt)
Podaj największą liczbę całkowitą, która należy do zbioru wartości
tej funkcji.
Odpowiedź:
max_{\in\mathbb{Z},\in ZW_f }=
(wpisz liczbę całkowitą)