Podgląd testu : lo2@zd-05-02-wykres-i-miej-zer-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-10816 ⋅ Poprawnie: 229/432 [53%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Prosta wyznaczona przez punkty A=(3,4) i
B=(-2,-2) określona jest równaniem
-6x+by+c=0.
Podaj liczby b i c.
Odpowiedzi:
| b | = |
(wpisz liczbę całkowitą) |
| c | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. 1 pkt ⋅ Numer: pr-10103 ⋅ Poprawnie: 2/3 [66%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
» Na rysunku przedstawiony jest fragment wykresu funkcji liniowej
f, przy czym
f(0)=-2 i
f(-4)=0.
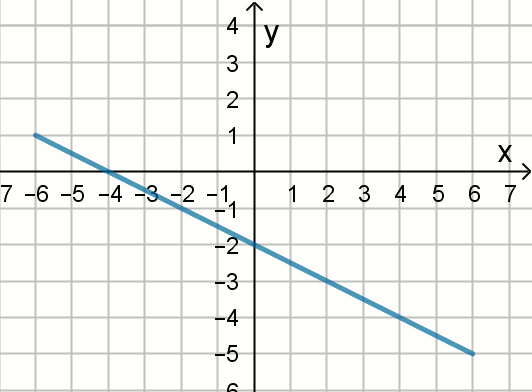

Wykres funkcji określonej wzorem g(x)=ax+b jest symetryczny do wykresu funkcji f względem prostej o równaniu y=x.
Wyznacz współczynniki a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę całkowitą) |
| b | = |
(wpisz liczbę całkowitą) |
| Zadanie 3. 2 pkt ⋅ Numer: pp-20306 ⋅ Poprawnie: 203/651 [31%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Dane są punkty A=(6, 72) i
B=(-7, -71). Wyznacz równanie prostej
AB.
Podaj współczynnik kierunkowy tej prostej.
Odpowiedź:
a=
(wpisz liczbę całkowitą)
Podpunkt 3.2 (1 pkt)
Wyznacz odciętą punktu przecięcia prostej AB
z osią Ox.
Odpowiedź:
| x_0= | |
| Zadanie 4. 2 pkt ⋅ Numer: pr-20032 ⋅ Poprawnie: 0/1 [0%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Funkcja f określona jest wzorem
f(x)=ax+b. Dla a=398
i b=399 oblicz
\frac{f(399)}{399^2}.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 4.2 (1 pkt)
Narysuj w układzie współrzędnych zbiór
A=\left\{(x,y): x\in\langle 1,3\rangle \wedge y=-\frac{1}{2}x+b \wedge b\in\langle -3,1\rangle\right\}
.
Podaj współrzędną y tego punktu należącego do zbioru A, który jest najbardziej oddalony od początku układu współrzędnych.
Odpowiedź:
| y= | |