Podgląd testu : lo2@zd-08-10-tr-podobne-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-11568 ⋅ Poprawnie: 40/61 [65%] | Rozwiąż |
Podpunkt 1.1 (0.5 pkt)
W trapezie podstawy mają długość 6 i
30, a wysokość ma długość 16.
Wyznacz odległości punktu przecięcia się przekątynych tego trapezu od jego podstaw.
Podaj krótszą z tych odległości.
Odpowiedź:
| min= | |
Podpunkt 1.2 (0.5 pkt)
Podaj dłuższą z tych odległości.
Odpowiedź:
| max= | |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10589 ⋅ Poprawnie: 105/165 [63%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
«« Pięciokąt ABCDE jest foremny.
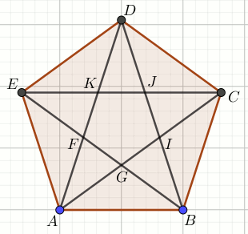
Który z trójkątów nie jest podobny do trójkąta ABD:
Odpowiedzi:
| A. ABG | B. ABI |
| C. BGI | D. EDB |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10584 ⋅ Poprawnie: 414/503 [82%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Przedstawione na rysunku trójkąty ABC i
PQR są podobne.
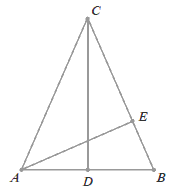
Oblicz długość boku AB trójkąta ABC.
Odpowiedź:
| |AB|= | |
| Zadanie 4. 2 pkt ⋅ Numer: pp-20917 ⋅ Poprawnie: 35/51 [68%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
» Trójkąt ABC jest prostokątny.
Na boku AC tego trójkąta zbudowano kwadrat,
natomiast bok AB przedłużono tak, że
|\angle EHA|=90^{\circ}.
Wiedząc, że |BC|=30 oraz bok kwadratu ma długość 16 oblicz pole powierzchni trójkąta EHA.
Odpowiedź:
| P_{\triangle EHA}= | |
| Zadanie 5. 2 pkt ⋅ Numer: pp-20869 ⋅ Poprawnie: 42/89 [47%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
Boki trójkąta rozwartokątnego ABC mają długości:
|AB|=20, |BC|=13 i
|AC|=11. Na boku AB zaznaczono
punkt D w taki sposób, że
|\sphericalangle CDB|=|\sphericalangle ACB|.
Oblicz długość odcinka CD.
Odpowiedź:
| |CD|= | |
Podpunkt 5.2 (1 pkt)
Oblicz długość odcinka DB.
Odpowiedź:
| |BD|= | |