⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-10-03-przes-wzdluz-oy-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-10769 ⋅ Poprawnie: 327/539 [60%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Na rysunku przedstawiony jest wykres funkcji
y=f(x).
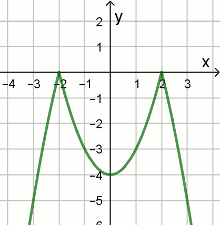
Które z równań ma dokładnie trzy rozwiązania:
Odpowiedzi:
| A. f(x-1)=4 | B. f(x+4)=-1 |
| C. f(x-4)+4=0 | D. f(x-4)=-1 |
| Zadanie 2. 1 pkt ⋅ Numer: pr-10376 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Wykres funkcji określonej wzorem f(x)=\frac{x}{x-1}
przesunięto o wektor \vec{u}=[-6,8], w wyniku czego
otrzymano wykres funkcji określonej wzorem g(x)=\frac{ax+b}{x+c}.
Podaj liczby a, b i c.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| c | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 3. 2 pkt ⋅ Numer: pp-20781 ⋅ Poprawnie: 172/657 [26%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« Dane są funkcje f oraz
g, przy czym
g(x)=f(x+5)-10. O funkcji f wiadomo, że
f(3)=-5 i f(-2)=-13.
Oblicz g(-2).
Odpowiedź:
g(-2)=
(wpisz liczbę całkowitą)
Podpunkt 3.2 (1 pkt)
Podaj wartość argumentu, dla którego funkcja g
przyjmuje wartość -23.
Odpowiedź:
x_0=
(wpisz liczbę całkowitą)
| Zadanie 4. 2 pkt ⋅ Numer: pp-20290 ⋅ Poprawnie: 130/346 [37%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Na rysunku przedstawiono fragment wykresu funkcji f,
który powstał w wyniku przesunięcia wykresu funkcji określonej wzorem
y=\frac{1}{x} dla każdej liczby rzeczywistej
x\neq 0.
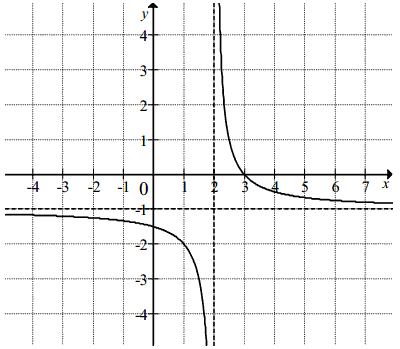
Odczytaj zbiór tych argumentów, dla których funkcja przyjmuje wartości dodatnie. Podaj liczbę występującą w środku tego zbioru.
Odpowiedź:
| Wpisz odpowiedź: | |
Podpunkt 4.2 (1 pkt)
Podaj miejsce zerowe funkcji g określonej wzorem
g(x)=f(x-2).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)