⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-10-04-symetrie-ox-oy-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-11398 ⋅ Poprawnie: 266/499 [53%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« O funkcji f wiadomo, że
D_f=\langle -2,3\rangle oraz
ZW_f=\langle 6,+\infty). O funkcji
g wiadomo, że
g(x)=-f(x).
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : ZW_g=(-\infty,-6) | T/N : D_g=\langle-2,3\rangle |
| T/N : D_g=\langle-3,2\rangle |
| Zadanie 2. 1 pkt ⋅ Numer: pp-10776 ⋅ Poprawnie: 205/612 [33%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Na rysunku 1 jest przedstawiony wykres funkcji
y=f(x).
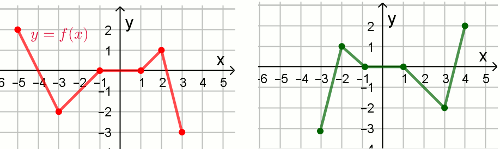
Funkcja przedstawiona na rysunku 2 jest określona wzorem:
Odpowiedzi:
| A. y=f(x-1) | B. y=-f(x) |
| C. y=f(-x) | D. żadnym z pozostałych wzorów |
| Zadanie 3. 1 pkt ⋅ Numer: pp-10767 ⋅ Poprawnie: 206/284 [72%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Na rysunkach przedstawiono wykresy dwóch funkcji
y=f(x) oraz
y=g(x):
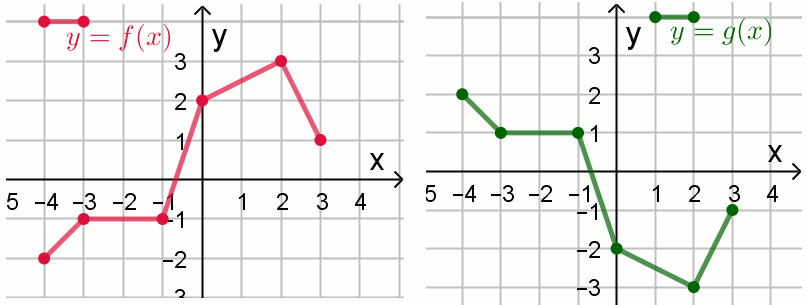
Funkcja f określona jest wzorem:
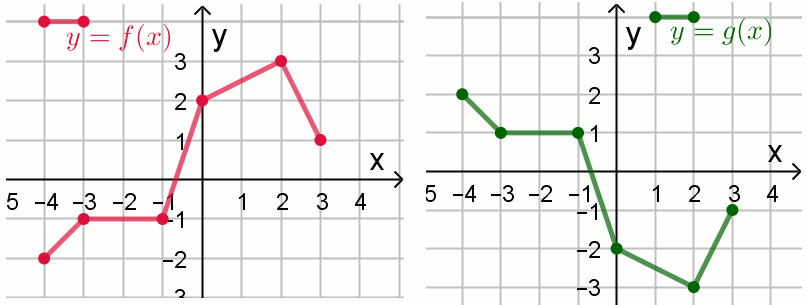
Odpowiedzi:
| A. f(x)=-g(-x) | B. f(x)=-g(x) |
| C. f(x)=g(x-1) | D. f(x)=g(-x) |
| Zadanie 4. 1 pkt ⋅ Numer: pp-11747 ⋅ Poprawnie: 35/41 [85%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
« W wyniku przekształcenia wykresu funkcji
f(x)=6x-2 przez symetrię względem osi
Ox otrzymamo wykres funkcji określonej
wzorem y=ax+b.
Podaj liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 5. 1 pkt ⋅ Numer: pp-11398 ⋅ Poprawnie: 266/499 [53%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
« O funkcji f wiadomo, że
D_f=\langle -2,3\rangle oraz
ZW_f=\langle 6,+\infty). O funkcji
g wiadomo, że
g(x)=-f(x).
Oceń prawdziwość poniższych zdań:
Odpowiedzi:
| T/N : ZW_g=(-\infty,6) | T/N : D_g=\langle-3,2\rangle |
| T/N : ZW_g=(-\infty,-6) |