Podgląd testu : lo2@zd-12-04-wykres-funkcji-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-10966 ⋅ Poprawnie: 34/59 [57%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Zbiorem wartości funkcji
y=-(x-3)(x+3)
określonej dla x\in(1,4\rangle jest pewien przedział liczbowy,
którego lewy koniec jest równy p, a prawy koniec jest równy
q.
Podaj liczby p i q.
Odpowiedzi:
| p | = |
(wpisz liczbę całkowitą) |
| q | = |
(wpisz liczbę całkowitą) |
| Zadanie 2. 1 pkt ⋅ Numer: pp-11534 ⋅ Poprawnie: 216/314 [68%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
(1 pkt)
Jeden z poniższych wzorów opisuje funkcję postaci
y=ax^2+bx+c, której wykres pokazano na rysunku:
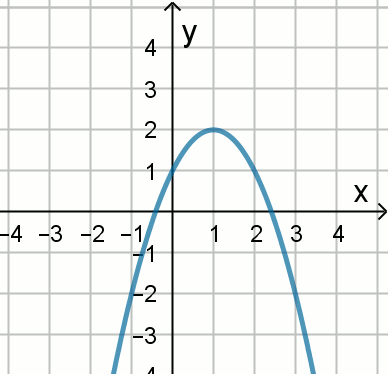

Wskaż ten wzór:
Odpowiedzi:
| A. y=a(x-1)^2+2 | B. y=a(x-1)^2-2 |
| C. y=a(x+1)^2+2 | D. y=a(x-2)^2+1 |
| E. y=a(x-2)^2-1 | F. y=a(x+1)^2-2 |
| Zadanie 3. 1 pkt ⋅ Numer: pp-11045 ⋅ Poprawnie: 41/79 [51%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Liczby a i b spełniają
warunek a\cdot b \lessdot 0.
Liczba rozwiązań układu równań \begin{cases} y=ax^2+b \\ y=0 \end{cases} jest równa:
Odpowiedzi:
| A. 3 | B. 0 |
| C. 1 | D. 2 |
| Zadanie 4. 2 pkt ⋅ Numer: pp-20349 ⋅ Poprawnie: 7/38 [18%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
«« Dana jest funkcja
f(x)=
\begin{cases}
(x+3)^2-6 \text{, dla } x\leqslant 0 \\
-(x+3)^2+12 \text{, dla }x > 0
\end{cases}
.
Wyznacz zbiór tych wartości, które funkcja f przyjmuje trzy razy, dla trzech różnych argumentów.
Zbiór ten zapisz w postaci przedziału. Podaj lewy koniec tego przedziału.
Odpowiedź:
x_l=
(wpisz liczbę całkowitą)
Podpunkt 4.2 (1 pkt)
Podaj prawy koniec tego przedziału.
Odpowiedź:
x_p=
(wpisz liczbę całkowitą)
| Zadanie 5. 2 pkt ⋅ Numer: pr-20060 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 5.1 (1 pkt)
» Wyznacz wzór funkcji jaką otrzymamy po przesunięciu wykresu funkcji
f(x)=-2x^2+4x+1 o wektor
\vec{u}=[p,q]. Zapisz wzór w postaci ogólnej y=ax^2+bx+c.
Podaj b.
Dane
p=-4
q=1
q=1
Odpowiedź:
b=
(wpisz liczbę całkowitą)
Podpunkt 5.2 (1 pkt)
Podaj c.
Odpowiedź:
c=
(wpisz liczbę całkowitą)