Podgląd testu : lo2@zd-13-02-prosta-i-okrag-pr
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11649 |
Podpunkt 1.1 (1 pkt)
W okręgu o promieniu 73 narysowano cięciwę,
która znajduje się w odległości 48
od środka tego okręgu.
Oblicz długość tej cięciwy.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11651 |
Podpunkt 2.1 (1 pkt)
Dwa promienie okręgu tworzą kąt środkowy tego okręgu o mierze 42^{\circ}.
Przez końce tych promieni położone na okręgu poprowadzono styczne do tego okręgu, które
przecięły się w punkcie P.
Wyznacz miarę stopniową kąta, pod którym widać ten okrąg z punktu P.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20951 |
Podpunkt 3.1 (2 pkt)
Z punktu P poprowadzono styczną do okręgu
o(O,r). Półprosta PO^{\rightarrow}
przecina ten okrąg w punktach A i B,
przy czym punkt B znajduje się 10
razy dalej od tej stycznej niż punkt A.
Jakim procentem promienia okręgu jest długość odcinka PA?
Odpowiedź:
| Wpisz odpowiedź: | |
| Zadanie 4. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20225 |
Podpunkt 4.1 (2 pkt)
W okręgu o środku O i promieniu długości
r poprowadzono dwie równoległe cięciwy
AB i CD w taki sposób,
że środek okręgu znajduje się pomiędzy tymi cięciwami:
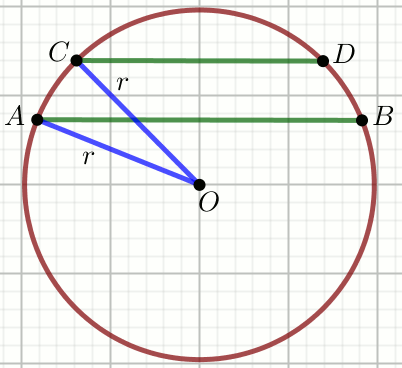
Oblicz odległość pomiędzy tymi cięciwami.
Dane
r=37
|CD|=70
|AB|=52
|CD|=70
|AB|=52
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)