Podgląd testu : lo2@zd-13-04-katy-i-kola-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-10486 ⋅ Poprawnie: 314/406 [77%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Punkt O jest środkiem okręgu na rysunku:
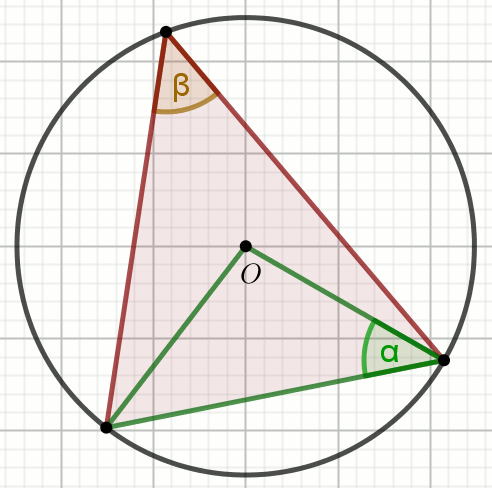
Wiedząc, że \alpha=39^{\circ}, wyznacz miarę stopniową kąta \beta.

Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 2. 1 pkt ⋅ Numer: pp-10511 ⋅ Poprawnie: 147/201 [73%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Kąt \alpha na rysunku ma miarę 62^{\circ}:
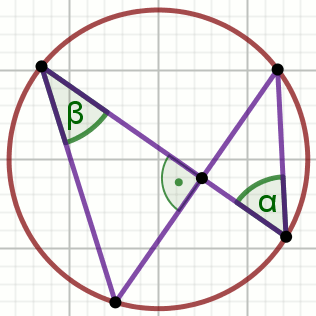

Wyznacz miarę stopniową kąta \beta zaznaczonego na rysunku.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 3. 1 pkt ⋅ Numer: pp-11414 ⋅ Poprawnie: 56/94 [59%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
» Trójkąt ABC jest równoramienny o podstawie
AB, odcinek CD
jest średnicą okręgu oraz \alpha=52^{\circ}:
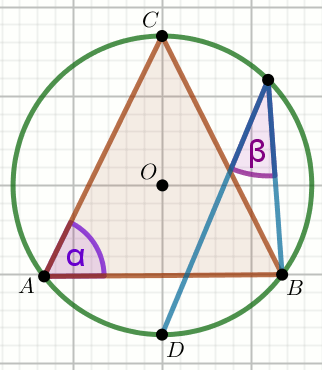

Wyznacz miarę stopniową kąta \beta.
Odpowiedź:
\beta=
(wpisz liczbę całkowitą)
| Zadanie 4. 2 pkt ⋅ Numer: pp-20783 ⋅ Poprawnie: 54/91 [59%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
Z punktu C leżącego poza okręgiem poprowadzono
sieczną okręgu zawierającą środek okręgu S oraz
taką sieczną przecinającą ten okrąg w punktach A
i B, że |SB|=|BC|.
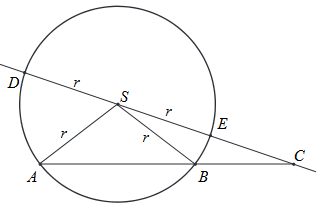

Oblicz |\sphericalangle ASD|.
Dane
|\sphericalangle BCE|=21^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. 2 pkt ⋅ Numer: pp-20809 ⋅ Poprawnie: 30/325 [9%] | Rozwiąż |
Podpunkt 5.1 (1 pkt)
(1 pkt) Punkt O jest środkiem, a odcinek
AC średnicą okręgu na rysunku.
W okrąg ten wpisano kąt ABC, a następnie odcinek
BC przedłużono do takiego punktu
D, że |BC|=|CD|.
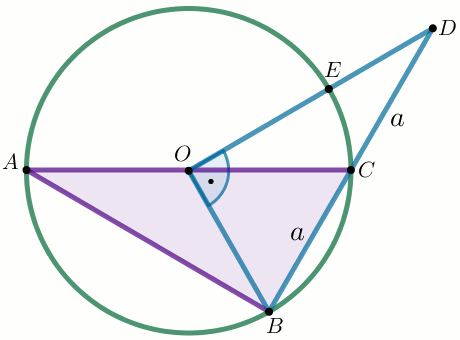

Wiedząc, że kąt BOD jest prosty, oblicz pole powierzchni trójkąta ABO.
Dane
a=20
Odpowiedź:
| P_{ABO}= | ||
| (wpisz trzy liczby całkowite) | ||
Podpunkt 5.2 (1 pkt)
(1 pkt) Łuk, na którym oparty jest mniejszy z kątów
środkowych okręgu AOE, ma długość
p\cdot\pi.
Wyznacz liczbę p.
Odpowiedź:
| p= | |