Podgląd testu : lo2@zd-13-07-okrag-wpisany-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-12095 ⋅ Poprawnie: 26/62 [41%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Dany jest trójkąt prostokątny ABC o bokach
|AC|=56, |BC|=33,
|AB|=65. Dwusieczne kątów tego trójkąta przecinają się w punkcie
P (zobacz rysunek).
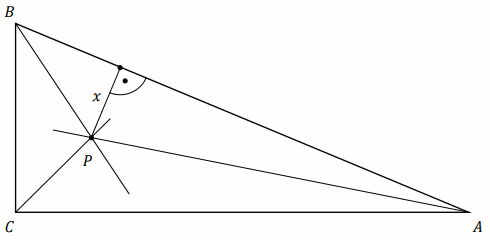

Odległość x punktu P od przeciwprostokątnej AB jest równa:
Odpowiedzi:
| A. \frac{21}{2} | B. \frac{25}{2} |
| C. 12 | D. 13 |
| E. 11 | F. \frac{27}{2} |
| Zadanie 2. 3 pkt ⋅ Numer: pp-21017 ⋅ Poprawnie: 17/51 [33%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
W trójkącie prostokątnym najkrótsza wysokość ma długość 108,
a najkrótszy bok ma długość 135.
Oblicz długości dwóch pozostałych boków tego trójkąta.
Odpowiedzi:
| min | = |
(wpisz liczbę całkowitą) |
| max | = |
(wpisz liczbę całkowitą) |
Podpunkt 2.2 (1 pkt)
Oblicz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
| R= | |
Podpunkt 2.3 (1 pkt)
Oblicz długość promienia okręgu wpisanego w ten okrąg.
Odpowiedź:
r=
(wpisz liczbę całkowitą)
| Zadanie 3. 4 pkt ⋅ Numer: pp-30015 ⋅ Poprawnie: 39/137 [28%] | Rozwiąż |
Podpunkt 3.1 (4 pkt)
«« Trójkąt ABC jest prostokątny i jedna z jego
przyprostokątnych jest dwa razy dłuższa od drugiej, a środkowa
CD ma długość d.
Wiedząc, że |\sphericalangle C|=90^{\circ} oblicz promień okręgu wpisanego w ten trójkąt.
Dane
d=2\sqrt{5}=4.472135954999579
Odpowiedź:
| r= |
|
|
| (wpisz cztery liczby całkowite) | ||
| Zadanie 4. 2 pkt ⋅ Numer: pr-20556 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 4.1 (1 pkt)
Dany jest trójkąt:
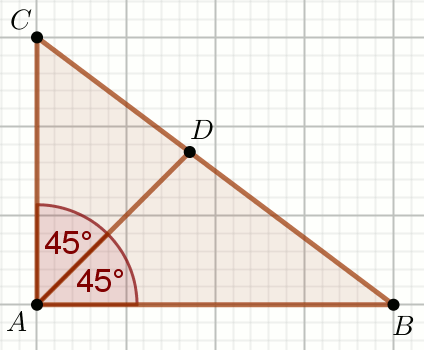

Oblicz |CD|.
Dane
|AC|=28
|AB|=45
|AB|=45
Odpowiedź:
| |CD|= | |
Podpunkt 4.2 (1 pkt)
Oblicz |DB|.
Odpowiedź:
| |BD|= | |