⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-16-02-tw-cosinusow-pr
| Zadanie 1. 2 pkt ⋅ Numer: pp-20888 ⋅ Poprawnie: 86/161 [53%] | Rozwiąż |
Podpunkt 1.1 (2 pkt)
« Oblicz długość środkowej trójkąta o bokach długości
5, 10 i
13, poprowadzonej do najdłuższego boku.
Odpowiedź:
| d= | |
| Zadanie 2. 2 pkt ⋅ Numer: pr-20747 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 2.1 (2 pkt)
« Trójkąt na rysunku jest równoboczny, a liczba k
jest równa 3:
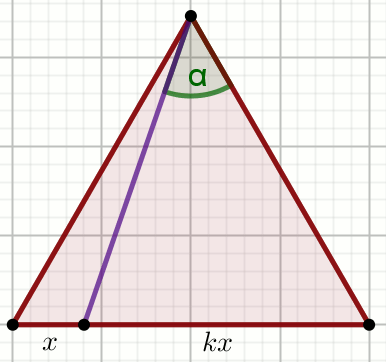
Oblicz \sin\alpha.
Odpowiedź:
| \sin\alpha= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 3. 4 pkt ⋅ Numer: pr-30379 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 3.1 (2 pkt)
«« Pole powierzchni trójkąta o kącie ostrym 30^{\circ} jest
równe 16\sqrt{3}, a promień okręgu na nim opisanego
ma długość 8.
Podaj długość najdłuższego boku tego trójkąta.
Odpowiedź:
a_{max}=
\cdot√
(wpisz dwie liczby całkowite)
(wpisz dwie liczby całkowite)
Podpunkt 3.2 (1 pkt)
Podaj długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
R=
(wpisz liczbę całkowitą)
Podpunkt 3.3 (1 pkt)
Podaj długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
| r= |
|
|
| (wpisz cztery liczby całkowite) | ||