Podgląd testu : lo2@zd-16-05-pole-troj-1-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-10654 ⋅ Poprawnie: 235/356 [66%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Oblicz pole powierzchni równoległoboku o bokach długości \frac{13}{11} i
10 oraz kącie ostrym o mierze
60^{\circ}.
Odpowiedź:
| P= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 2. 1 pkt ⋅ Numer: pp-11545 ⋅ Poprawnie: 55/150 [36%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
(1 pkt)
Trójkąt ABC ma pole powierzchni równe 648.
Na bokach AB i AC tego trójkąta zaznaczono punkty odpowiednio
D i E takie, że |DB|=\frac{1}{3}|AB|
oraz |EC|=\frac{1}{2}|AC|:
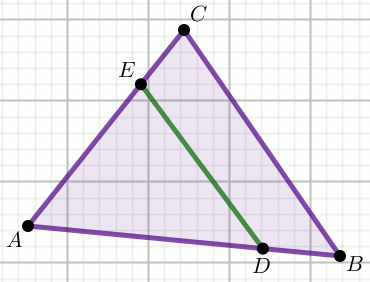
Pole powierzchni trójkąta ADE jest równe:

Odpowiedzi:
| A. 324 | B. 162 |
| C. \frac{864}{5} | D. 216 |
| E. 144 | F. 270 |
| Zadanie 3. 2 pkt ⋅ Numer: pp-20284 ⋅ Poprawnie: 18/39 [46%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
» We wnętrzu trójkąta równobocznego o boku długości 9\sqrt{2}
zaznaczono dowolny punkt.
Oblicz sumę odległości tego punktu od wszystkich boków tego trójkąta.
Odpowiedź:
| d= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 4. 3 pkt ⋅ Numer: pr-20879 ⋅ Poprawnie: 0/1 [0%] | Rozwiąż |
Podpunkt 4.1 (1 pkt)
(1 pkt)
W trójkącie równoramiennym ABC punkt
E dzieli wysokość CD tego trójkąta
w stosunku |CE|:|ED|=4:1. Przez punkt E
poprowadzono prostopadłą do boku BC, która przecięła ten bok
w punkcie F (zobacz rysunek):
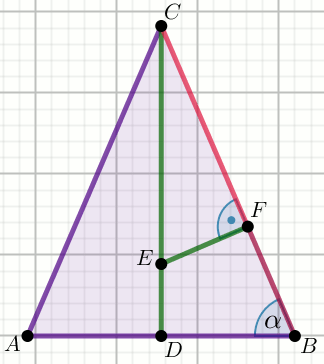

Wiedząc, że \cos\alpha=\frac{28}{53}, oblicz
o ile procent ramię trójkąta BC
jest dłuższe od wysokości CD.
Wynik zapisz bez znaku procenta.
Odpowiedź:
| Wpisz odpowiedź: | |
Podpunkt 4.2 (2 pkt)
(2 pkt)
Oblicz jakim procentem pola powierzchni trójkąta ABC
jest pole powierzchni czworokąta BDFE.
Wynik zapisz bez znaku procenta.
Wynik zapisz bez znaku procenta.
Odpowiedź:
| Wpisz odpowiedź: | |