⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-16-06-pole-troj-2-pr
| Zadanie 1. 2 pkt ⋅ Numer: pp-21028 ⋅ Poprawnie: 23/40 [57%] | Rozwiąż |
Podpunkt 1.1 (2 pkt)
« Pole powierzchni trójkąta jest równe 1170, a promień
okręgu wpisanego w ten trójkąt ma długość 15.
Wiedząc, że długości boków tego trójkąta są kolejnymi liczbami naturalnymi, oblicz długość najdłuższej wysokości tego trójkąta.
Odpowiedź:
| h_{min}= | |
| Zadanie 2. 2 pkt ⋅ Numer: pp-20907 ⋅ Poprawnie: 42/115 [36%] | Rozwiąż |
Podpunkt 2.1 (1 pkt)
Podstawa trójkąta równoramiennego ma długość 80, a pole
powierzchni tego trójkąta jest równe 360.
Oblicz długość ramienia tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(wpisz liczbę całkowitą)
Podpunkt 2.2 (1 pkt)
Wyznacz długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
| R= | |
| Zadanie 3. 4 pkt ⋅ Numer: pp-30020 ⋅ Poprawnie: 35/120 [29%] | Rozwiąż |
Podpunkt 3.1 (4 pkt)
« Każdy bok trójkąta podzielono dwoma punktami na odcinki, których długości
mają się do siebie jak a:b:a. Pole powierzchni
tego trójkąta jest równe P.
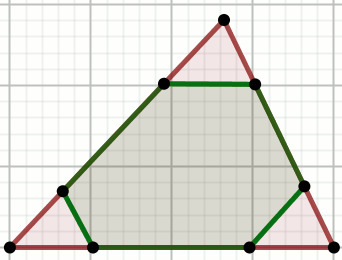
Wyznacz pole sześciokąta, którego wierzchołkami są punkty podziałów boków trójkąta.
Dane
a=2
b=3
P=49
b=3
P=49
Odpowiedź:
P=
(wpisz liczbę całkowitą)