⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-16-07-pola-tr-pod-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-10515 ⋅ Poprawnie: 92/170 [54%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
« Obwody dwóch trójkątów podobnych, których pola pozostają w stosunku
49:121, mogą być równe:
Odpowiedzi:
| A. 14:\frac{147}{11} | B. 33:14 |
| C. 7:\frac{49}{11} | D. 7:\frac{121}{7} |
| Zadanie 2. 2 pkt ⋅ Numer: pp-20756 ⋅ Poprawnie: 57/207 [27%] | Rozwiąż |
Podpunkt 2.1 (2 pkt)
« Dane są punkty na okręgu:
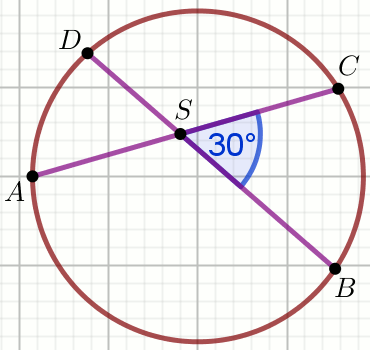
Oblicz P_{\triangle ASD}.
Dane
|AS|=17
|SB|=9
|SC|=13
|SB|=9
|SC|=13
Odpowiedź:
| P_{\triangle ASD}= | |
| Zadanie 3. 2 pkt ⋅ Numer: pp-20903 ⋅ Poprawnie: 19/36 [52%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
W trapezie ABCD, AB\parallel CD, poprowadzono przekątne,
które przecięły się w punkcie E. Pola powierzchni trójkątów
ABE i BCE są równe odpowiednio
32 i 20.
Oblicz pole powierzchni trójkąta CDE.
Odpowiedź:
| P_{\triangle CDE}= | |