⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-16-08-pole-kola-wyc-odc-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-11598 ⋅ Poprawnie: 48/118 [40%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Promień koła ma długość 9, a kąt wycinka tego koła ma miarę
90^{\circ}. Oblicz pole powierzchni tego wycinka i zapisz wynik w postaci
p\cdot\pi.
Podaj liczbę p.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. 2 pkt ⋅ Numer: pp-20766 ⋅ Poprawnie: 77/170 [45%] | Rozwiąż |
Podpunkt 2.1 (2 pkt)
W wycinek kołowy o kącie środkowym \alpha
wpisano okrąg o polu powierzchni P:
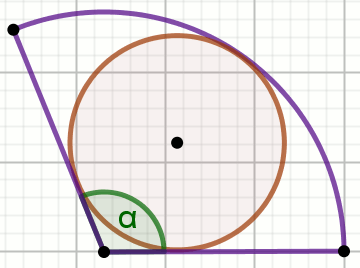
Oblicz pole powierzchni tego wycinka.
Dane
\alpha=120^{\circ}
P=36\pi=113.09733552923256
P=36\pi=113.09733552923256
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 2 pkt ⋅ Numer: pp-20763 ⋅ Poprawnie: 11/49 [22%] | Rozwiąż |
Podpunkt 3.1 (2 pkt)
Punkt O jest środkiem okręgu, a niebieski trójkąt
jest równoboczny:
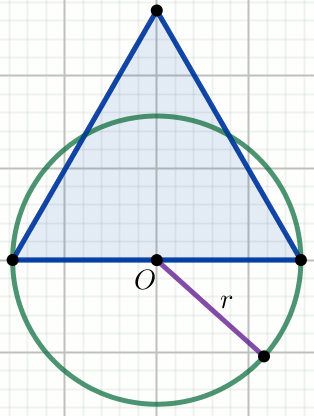
Oblicz pole powierzchni części koła leżącej poza trójkątem.
Dane
r=4\sqrt{11}=13.26649916142160
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)