Podgląd testu : lo2@zd-21-03-rownolegloboki-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-11096 ⋅ Poprawnie: 171/341 [50%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
W romb o boku długości \frac{14\sqrt{3}}{11} i kącie rozwartym
150^{\circ} wpisano okrąg.
Oblicz długość promienia tego okręgu.
Odpowiedź:
| r= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 2. 2 pkt ⋅ Numer: pp-20451 ⋅ Poprawnie: 31/85 [36%] | Rozwiąż |
Podpunkt 2.1 (2 pkt)
Przekątne prostokąta mają długość 72 i przecinają
sie w punkcie E oraz
|EF|=27.
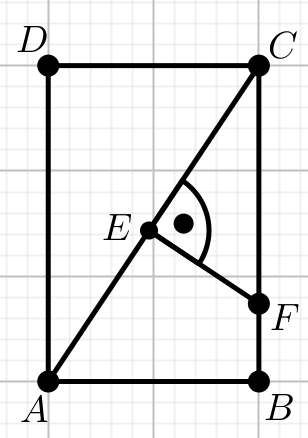

Oblicz długość odcinka BF.
Odpowiedź:
| |BF|= | |
| Zadanie 3. 2 pkt ⋅ Numer: pr-20125 ⋅ Poprawnie: 0/2 [0%] | Rozwiąż |
Podpunkt 3.1 (1 pkt)
« W równoległoboku |AB|=21 i
|AE|=|DE|=5:
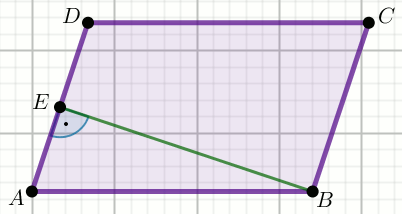

Oblicz długość krótszej przekątnej tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 3.2 (1 pkt)
Oblicz długość dłuższej przekątnej tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. 2 pkt ⋅ Numer: pr-30096 ⋅ Poprawnie: 0/1 [0%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
« Czworokąt na rysunku jest prostokątem
(x \lessdot y):
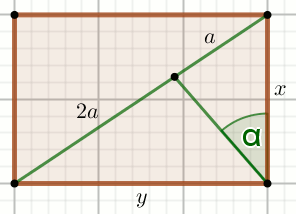

Oblicz \sin\alpha.
Dane
x=33
y=56
y=56
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)