⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-22-01-prostokaty-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-11494 ⋅ Poprawnie: 241/293 [82%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Pole kwadratu ABCDjest równe
196. Kwadrat KLMN
jest obrazem kwadratu ABCD w podobieństwie o skali
k=\frac{1}{3}.
Oblicz długość przekątnej kwadratu KLMN.
Odpowiedź:
| |KM|= | ||
| (wpisz trzy liczby całkowite) | ||
| Zadanie 2. 4 pkt ⋅ Numer: pp-30115 ⋅ Poprawnie: 15/61 [24%] | Rozwiąż |
Podpunkt 2.1 (2 pkt)
« Punkty M i N na poniższym
rysunku są środkami boków kwadratu ABCD o boku
długości a.
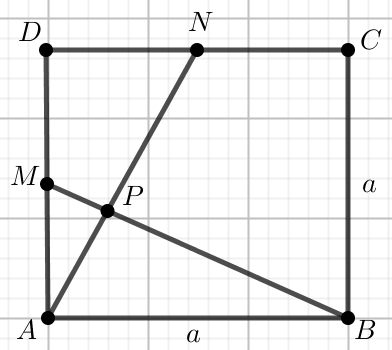
Oblicz miarę stopniową kąta APM.
Dane
a=8
Odpowiedź:
|\sphericalangle APM|\ [^{\circ}]=
(wpisz liczbę całkowitą)
Podpunkt 2.2 (2 pkt)
Oblicz pole czworokąta BCNP.
Odpowiedź:
| P_{BCNP}= | |
| Zadanie 3. 2 pkt ⋅ Numer: pr-20146 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 3.1 (1 pkt)
Pole powierzchni prostokąta wynosi 840. Długość
jednego boku tego prostokąta zmniejszono o 4,
a długość drugiego boku zwiększono o 5. Wówczas
okazało się, że pole powierzchni prostokąta nie uległo zmianie.
Jaką długość miał krótszy bok tego prostokąta?
Odpowiedź:
min=
(wpisz liczbę całkowitą)
Podpunkt 3.2 (1 pkt)
Jaką długość miał dłuższy bok tego prostokąta?
Odpowiedź:
max=
(wpisz liczbę całkowitą)
| Zadanie 4. 4 pkt ⋅ Numer: pr-30113 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 4.1 (4 pkt)
Czworokąt na rysunku jest prostokątem:
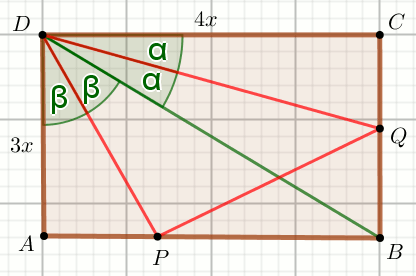
Oblicz \frac{P_{ABCD}}{P_{PQD}}.
Odpowiedź:
| \frac{P_{ABCD}}{P_{PQD}}= | |