Podgląd testu : lo2@zd-22-02-rownolegloboki-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-11093 ⋅ Poprawnie: 197/253 [77%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
» Koło K ma promień
r, trójkąt równoboczny
T ma bok długości a,
trójkąt P ma boki 3,4,5,
zaś romb R ma obwód
L i kąt ostry 45^{\circ}.
Wskaż tą figurę, która ma największe pole powierzchni:
Dane
r=6\sqrt{2}=8.48528137423857
a=6\sqrt{2}=8.48528137423857
L=8
a=6\sqrt{2}=8.48528137423857
L=8
Odpowiedzi:
| A. R | B. K |
| C. P | D. T |
| Zadanie 2. 2 pkt ⋅ Numer: pp-20457 ⋅ Poprawnie: 33/96 [34%] | Rozwiąż |
Podpunkt 2.1 (2 pkt)
Czworokąt na rysunku jest równoległobokiem:
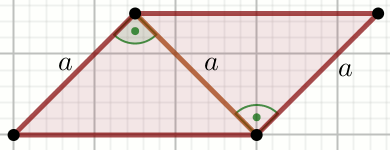

Oblicz pole powierzchni tego równoległoboku.
Dane
a=\frac{9\sqrt{2}}{2}=6.36396103067893
Odpowiedź:
| P= | |
| Zadanie 3. 4 pkt ⋅ Numer: pp-30121 ⋅ Poprawnie: 17/71 [23%] | Rozwiąż |
Podpunkt 3.1 (4 pkt)
« Okrąg przechodzi przez wierzchołek kąta ostrego i dwa wierzchołki kątów
rozwartych rombu. Okrąg podzielił dłuższą przekątną tego rombu na odcinki o
długościach 29 i 21.
Wyznacz pole powierzchni tego rombu.
Odpowiedź:
P=
(wpisz liczbę całkowitą)
| Zadanie 4. 2 pkt ⋅ Numer: pr-20149 ⋅ Poprawnie: 2/2 [100%] | Rozwiąż |
Podpunkt 4.1 (2 pkt)
« Czworokąt na rysunku jest równoległobokiem:
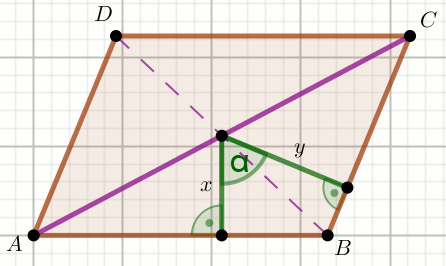

Oblicz jego pole powierzchni.
Dane
x=\frac{63}{2}=31.5000000000
y=21
\alpha=60^{\circ}=60
y=21
\alpha=60^{\circ}=60
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)