⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-22-03-trapezy-pr
| Zadanie 1. 1 pkt ⋅ Numer: pp-11488 ⋅ Poprawnie: 188/221 [85%] | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Odcinek łączący środki ramion trapezu o wysokości ......... cm ma długość
\frac{15}{2} cm, a pole
powierzchni tego trapezu jest równe
\frac{75}{2} cm2.
Podaj brakującą liczbę.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. 2 pkt ⋅ Numer: pp-20472 ⋅ Poprawnie: 53/138 [38%] | Rozwiąż |
Podpunkt 2.1 (2 pkt)
Wysokość trapezu równoramiennego wynosi h, a sinus
kąta ostrego tego trapezu jest równy \frac{p}{q}.
Stosunek długości podstaw tego trapezu jest równy
1:3.
Oblicz pole tego trapezu.
Dane
h=48
p=48
q=73
p=48
q=73
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. 2 pkt ⋅ Numer: pr-20170 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 3.1 (1 pkt)
W trapez prostokątny ABCD o stosunku boków
|BC|:|AD|=15:17 wpisano okrąg o promieniu
długości 12:
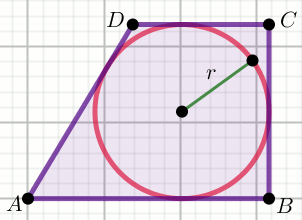
Oblicz obwód tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 3.2 (1 pkt)
Oblicz pole powierzchni tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. 4 pkt ⋅ Numer: pr-30131 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 4.1 (1 pkt)
» Na trapezie ABCD opisano okrąg o środku w punkcie
O, w taki sposób, że dłuższa
podstawa tego trapezu jest średnicą okręgu. Odcinki AD i
OC mają równą długość wynoszącą 9\sqrt{2}:
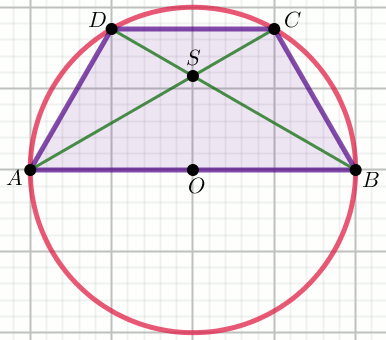
Oblicz wysokość tego trapezu.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 4.2 (1 pkt)
Oblicz |CD|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 4.3 (1 pkt)
Wyznacz P_{\triangle ABS}.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 4.4 (1 pkt)
Wyznacz długość promienia okręgu wpisanego w trójkąt ABS.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)