⇒ Matury CKE
⇒ Rankingi
⇒ Wyniki uczniów
♦ Testy i arkusze
♦ Działy
♦ Rozwiązalność
⇒ Strona główna
⇒ Zaloguj mnie
Podgląd testu : lo2@zd-23-13-monotonicznosc-pr
| Zadanie 1. 1 pkt ⋅ Numer: pr-10357 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 1.1 (1 pkt)
Na rysunku przedstawiono fragment wykresu pochodnej
y=f'(x) funkcji y = f(x):
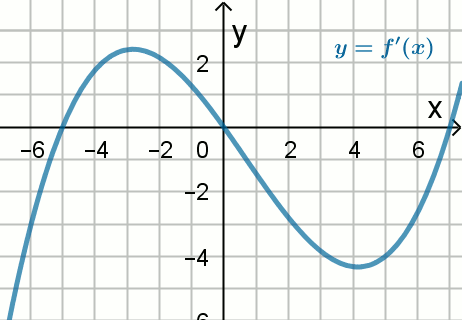
Wynika stąd, że:
Odpowiedzi:
| A. f(7) > f(0) | B. f(-5) \lessdot f(0) |
| C. f(-6) \lessdot f(-5) | D. f(6) > f(5) |
| Zadanie 2. 1 pkt ⋅ Numer: pr-10359 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 2.1 (1 pkt)
« Rysunek przedstawia wykres funkcji
y=f'(x):
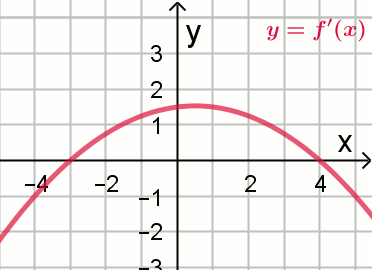
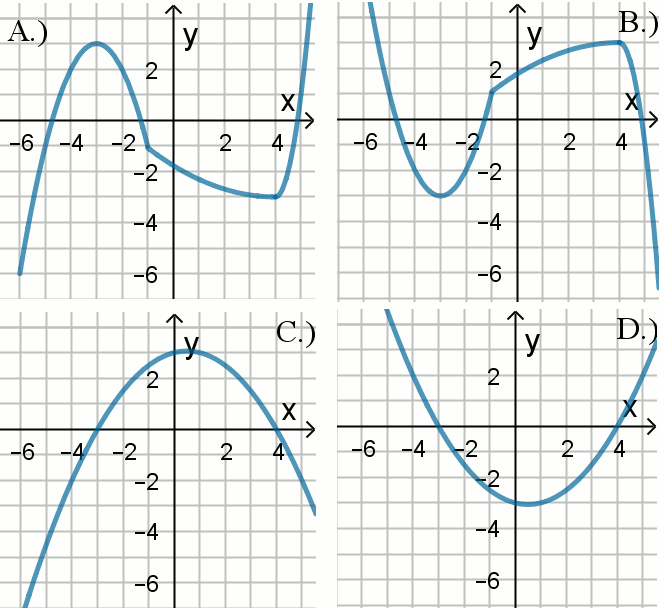
Jeden z poniższych rysunków przedstawia wykres funkcji f.
Który:
Odpowiedzi:
| A. B | B. D |
| C. A | D. C |
| Zadanie 3. 2 pkt ⋅ Numer: pr-20862 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 3.1 (1 pkt)
» Wyznacz przedziały monotoniczności funkcji
f(x)=\frac{x-a}{(x-b)^2}
.
Podaj lewy koniec przedziału, w którym funkcja ta rośnie.
Dane
a=3
b=-4
b=-4
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 3.2 (1 pkt)
Podaj prawy koniec przedziału, w którym funkcja ta rośnie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. 2 pkt ⋅ Numer: pr-20864 ⋅ Poprawnie: 0/0 | Rozwiąż |
Podpunkt 4.1 (2 pkt)
Wyznacz przedziały monotoniczności funkcji
f(x)=\frac{x^4}{(x-1)^2}.
Podaj sumę prawych końców tych wszystkich przedziałów, w których funkcja ta jest malejąca.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)