Rozwiązywanie prostych równań
Zadania dla klasy pierwszej liceum ogólnokształcącego - poziom podstawowy
- zbiory liczbowe
- suma zbiorów
- iloczyn zbiorów
- cześć wspólna zbiorów
- opisywanie zbiorów
- diagramy Vienna
- dopełnienie zbioru
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10032 |
Podpunkt 1.1 (1 pkt)
Przyjmując, że liczba 0 jest liczbą naturalną
wskaż zbiór, który jest równy zbiorowi:
A=\{n\in \mathbb{N}: n^2\leqslant 9\}
Odpowiedzi:
| A. \{-3,-2,-1,...,3\} | B. \{-3,3\} |
| C. \{1,2,3,...,3\} | D. \{0,1,2,...,3\} |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10036 |
Podpunkt 2.1 (1 pkt)
Wyznacz liczbę największą w zbiorze:
A=\{n: n \in \mathbb{C} \wedge n=2k+1 \wedge k \in \mathbb{C} \wedge k \leqslant 7 \}.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10037 |
Podpunkt 3.1 (1 pkt)
Dany jest zbiór
A=\left\lbrace n\in \mathbb{C}: (2n-1\geqslant 3) \wedge (n \lessdot 10)\right\rbrace
.
Wyznacz \overline{\overline{A}} (ilość elementów zbioru).
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10038 |
Podpunkt 4.1 (1 pkt)
Dany jest zbiór
A=\left\lbrace n\in \mathbb{C}: (2n-1\geqslant 9) \wedge (n \lessdot 17)\right\rbrace
.
Wyznacz najmiejszą liczbę w tym zbiorze.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10039 |
Podpunkt 5.1 (1 pkt)
Wskaż zbiór, który jest równy zbiorowi:
A=\{k\in \mathbb{C}: k^2-1=8\}
.
Odpowiedzi:
| A. \left\lbrace -3,3\right\rbrace | B. \left\lbrace 1,2,3,...,3\right\rbrace |
| C. \left\lbrace 0,1,2,...,3\right\rbrace | D. \left\lbrace -3,-2,-1,...,3\right\rbrace |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10040 |
Podpunkt 6.1 (1 pkt)
» Wyznacz ilość elementów zbioru:
A=\{x: x \in \mathbb{N} \wedge (-3\lessdot x \lessdot 4)\}
.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10041 |
Podpunkt 7.1 (1 pkt)
Znajdź najmniejszą liczbę w zbiorze
A=\{n: n \in \mathbb{C} \wedge n=2k+1 \wedge k \in \mathbb{C} \wedge k > 5 \}
.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10042 |
Podpunkt 8.1 (1 pkt)
» Znajdź najmniejszą liczbę w zbiorze
A=\{k: k \in \mathbb{C} \wedge k\lessdot 15 \wedge \text{ (k - liczba pierwsza)}\}
.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10043 |
Podpunkt 9.1 (1 pkt)
« Dany jest zbiór
A=\left\lbrace n\in \mathbb{N}:\frac{5}{n}-2\in\mathbb{N} \right\rbrace
.
Wyznacz ilość elementów zbioru A.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10033 |
Podpunkt 10.1 (1 pkt)
Dany jest zbiór
A=\left\lbrace n\in\mathbb{N}:\frac{10}{n}-n\in\mathbb{N} \right\rbrace
.
Wyznacz ilość elementów zbioru A.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10034 |
Podpunkt 11.1 (1 pkt)
» Dany jest zbiór
A=\left\lbrace m\in \mathbb{C}:\frac{12}{m}+2\in\mathbb{N} \right\rbrace
.
Wyznacz ilość elementów zbioru A.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10035 |
Podpunkt 12.1 (1 pkt)
» Dany jest zbiór
A=\left\lbrace m\in \mathbb{C}:\frac{10}{m}-m\in\mathbb{N} \right\rbrace
.
Wyznacz ilość elementów zbioru A.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 13. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10027 |
Podpunkt 13.1 (1 pkt)
» Dane są zbiory A i B
takie, że B-A=\emptyset.
Wówczas:
Odpowiedzi:
| A. A-B=\emptyset | B. A\subset B |
| C. A\cap B=B | D. A\cup B=B |
| Zadanie 14. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10028 |
Podpunkt 14.1 (1 pkt)
Dane sa zbiory A i B
takie, że A \cap B=\emptyset.
Wówczas:
Odpowiedzi:
| A. A\cup B=B | B. A-B=A |
| C. A-B=\emptyset | D. B-A=A |
| E. A\cup B=A | F. B\subset A |
| Zadanie 15. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10029 |
Podpunkt 15.1 (1 pkt)
Na diagramie zaznaczono zbiór:
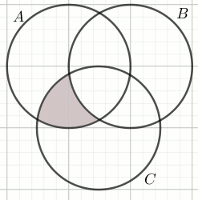

Odpowiedzi:
| A. (A\cap C)-B | B. A\cup C |
| C. A\cap C | D. (A\cup C)-B |
| Zadanie 16. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10030 |
Podpunkt 16.1 (1 pkt)
« W pewnej szkole jest 72 uczniów.
4 osób uczy się tylko języka francuskiego,
4 osób tylko angielskiego, 7
osób tylko niemieckiego, 8 osób tylko francuskiego i
angielskiego, 9 osób tylko francuskiego i niemieckiego,
4 osób tylko niemieckiego i angielskiego, a
3 osób wszystkich trzech języków.
Ilu uczniów nie uczy się żadnego z tych języków?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10031 |
Podpunkt 17.1 (1 pkt)
Niech dana będzie przestrzeń U oraz zbiory
A i B
zawarte w przestrzeni U:
U=\{1, 2, 3, 4, 5, 6, 7, 8, 9\}\\
A=\{2, 4, 6, 8\}\\
B=\{2, 5, 7\}
Które z poniższych zdań są zdaniami prawdziwymi?
Odpowiedzi:
| T/N : A-B\subset A | T/N : \overline{\overline{A - B}}=3 |
| T/N : B'=\{1,3,4,6,8,9\} | T/N : \overline{\overline{B - A}}=2 |
| Zadanie 18. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10044 |
Podpunkt 18.1 (1 pkt)
» Dane są zbiory:
T - zbiór trapezów R - zbiór równoległoboków K - zbiór kwadratów P - zbiór prostokątów
Które z podanych zdań są prawdziwe?
Odpowiedzi:
| T/N : K \cap T = K | T/N : K-P = R |
| T/N : P - R = \emptyset | T/N : K \subset R |
| Zadanie 19. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10045 |
Podpunkt 19.1 (1 pkt)
» Dane są zbiory:
T - zbiór trójkątów R - zbiór trójkątów równoramiennych B - zbiór trójkątów równobocznych P - zbiór trójkątów prostokątnych
Które z podanych zdań są prawdziwe?
Odpowiedzi:
| T/N : R \cap P\neq \emptyset | T/N : (R\cup B\cup P)'=T |
| T/N : P \subset R | T/N : R\cup B\cup P=T |
| Zadanie 20. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20006 |
Podpunkt 20.1 (1 pkt)
Spośród n uczniów klasy pierwszej,
a trenuje siatkówkę,
b koszykówkę, a c
jednocześnie siatkówkę i koszykówkę.
Ilu uczniów nie trenuje żadnej z wymienionych dyscyplin?
Dane
n=29
a=15
b=16
c=7
a=15
b=16
c=7
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 20.2 (1 pkt)
Ilu uczniów trenuje tylko jedną z wymienionych dyscyplin?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 21. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20007 |
Podpunkt 21.1 (1 pkt)
« Niech A oznacza zbiór liczb naturalnych nieparzystych, mniejszych
od 15, zaś B zbiór
naturalnych dzielników liczby 156. Wyznacz
A\cap B.
Ile elementów zawiera ten zbiór?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 21.2 (1 pkt)
Ile jest równa suma tych liczb?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)