Wartość bezwzględna
Zadania dla klasy pierwszej liceum ogólnokształcącego - poziom podstawowy
- definicja wartości bezwzględnej
- podstawowe wzory
- interpretacja geometryczna wartości bezwzględnej
- proste równania i nierówności i wartością bezwzględną
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10184 |
Podpunkt 1.1 (1 pkt)
Oceń, które z poniższych równości są prawdziwe dla każdej liczby rzeczywistej
x:
Odpowiedzi:
| T/N : |x-2|=|-x-2| | T/N : |-x|=x |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11557 |
Podpunkt 2.1 (1 pkt)
Wartość wyrażenia
\sqrt{\left(1+\sqrt{a}\right)^2}-\sqrt{\left(1-\sqrt{a}\right)^2}
jest równa 2\sqrt{\stackrel{\ }{.....}}.
Podaj brakującą liczbę.
Dane
a=11
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10182 |
Podpunkt 3.1 (1 pkt)
Oblicz wartość wyrażenia \frac{|7-12|}{-2}.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11572 |
Podpunkt 4.1 (1 pkt)
» Wartość wyrażenia |a-x|-x-b dla
x\in (a, +\infty) można zapisać w postaci
mx+n, gdzie m,n\in\mathbb{Z}.
Podaj liczby m i n.
Dane
a=12
b=6
b=6
Odpowiedzi:
| m | = |
(wpisz liczbę zapisaną dziesiętnie) |
| n | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 5. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10180 |
Podpunkt 5.1 (1 pkt)
Dla każdej liczby x spełniającej warunek
-15 \lessdot x \lessdot 0, wyrażenie
\frac{|x+15|-x+15}{x} jest równe
\frac{mx+n}{x}, gdzie m,n\in\mathbb{Z}.
Podaj liczby m i n.
Odpowiedzi:
| m | = |
(wpisz liczbę zapisaną dziesiętnie) |
| n | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 6. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10185 |
Podpunkt 6.1 (1 pkt)
Wskaż liczbę, która spełnia równanie |ax+b|=cx:
Dane
a=10
b=4
c=12
b=4
c=12
Odpowiedzi:
| A. 1 | B. 4 |
| C. 3 | D. 2 |
| Zadanie 7. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10181 |
Podpunkt 7.1 (1 pkt)
» Jeżeli x\in(-\infty,0), to wyrażenie
||x|+12| można zapisać w postaci
mx+n, gdzie m,n\in\mathbb{Z}.
Podaj liczby m i n.
Odpowiedzi:
| m | = |
(wpisz liczbę zapisaną dziesiętnie) |
| n | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 8. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11558 |
Podpunkt 8.1 (1 pkt)
« Ile liczb całkowitych należy do dziedziny równania
\frac{x^2-6}{\sqrt{8-x}}+\sqrt{11-|x|}=0?
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11559 |
Podpunkt 9.1 (1 pkt)
Równanie |x-a|-b=0:
Dane
a=7
b=-2
b=-2
Odpowiedzi:
| A. ma więcej niż dwa rozwiązania | B. ma dokładnie dwa rozwiązania |
| C. nie ma rozwiązań | D. ma dokładnie jedno rozwiązanie |
| Zadanie 10. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10197 |
Podpunkt 10.1 (1 pkt)
Wskaż liczbę, która spełnia równanie:
\left| ax-4 \right| = 5-2ax
Dane
a=10
Odpowiedzi:
| A. -\frac{3}{20} | B. -\frac{1}{10} |
| C. \frac{1}{20} | D. \frac{1}{10} |
| Zadanie 11. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10186 |
Podpunkt 11.1 (0.2 pkt)
» Rozwiązaniem nierówności
|x-a| \lessdot b
jest zbiór liczb postaci:
Dane
a=8
b=5
b=5
Odpowiedzi:
| A. \langle p,q\rangle | B. (-\infty,p)\cup(q,+\infty) |
| C. (p,q) | D. (-\infty,p\rangle \cup \langle q,+\infty) |
| E. (p,q\rangle | F. \langle p,q) |
Podpunkt 11.2 (0.8 pkt)
Rozwiązanie nierówności zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców
liczbowych tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10188 |
Podpunkt 12.1 (0.2 pkt)
Rozwiązaniem nierówności
|x+a| \leqslant b
jest zbiór liczb postaci:
Dane
a=8
b=5
b=5
Odpowiedzi:
| A. (-\infty,p)\cup(q,+\infty) | B. \langle p,q\rangle |
| C. (-\infty,p\rangle \cup \langle q,+\infty) | D. \langle p,+\infty) |
| E. (p,q\rangle | F. (-\infty,q\rangle |
Podpunkt 12.2 (0.8 pkt)
Rozwiązanie nierówności zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców
liczbowych tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 13. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10189 |
Podpunkt 13.1 (0.2 pkt)
Rozwiązaniem nierówności
|x+a| \geqslant b
jest zbiór liczbowy postaci:
Dane
a=8
b=5
b=5
Odpowiedzi:
| A. (-\infty,p\rangle \cup \langle q,+\infty) | B. (p,q) |
| C. \langle p,+\infty) | D. \langle p,q) |
| E. \langle p,q\rangle | F. (-\infty,p)\cup(q,+\infty) |
Podpunkt 13.2 (0.8 pkt)
Rozwiązanie nierówności zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców
liczbowych tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 14. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10190 |
Podpunkt 14.1 (0.2 pkt)
Rozwiązaniem nierówności
|x-a| > b
jest zbiór liczbowy postaci:
Dane
a=8
b=5
b=5
Odpowiedzi:
| A. (p,q) | B. (p,q\rangle |
| C. \langle p,q) | D. \langle p,q\rangle |
| E. (-\infty,p)\cup(q,+\infty) | F. (-\infty,p\rangle \cup \langle q,+\infty) |
Podpunkt 14.2 (0.8 pkt)
Rozwiązanie nierówności zapisz w postaci sumy przedziałów. Podaj najmniejszy z końców liczbowych
tych przedziałów.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 15. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10191 |
Podpunkt 15.1 (1 pkt)
« Wskaż nierówność, której rozwiązaniem jest zbiór
\left(-\infty, \frac{a}{2}\right)\cup\left(\frac{b}{2},+\infty\right)
:
Dane
a=-4
b=6
b=6
Odpowiedzi:
| A. \left|x-\frac{1}{2}\right| \lessdot \frac{5}{2} | B. \left|x-\frac{1}{2}\right| > \frac{5}{2} |
| C. \left|x+\frac{1}{2}\right| \leqslant \frac{5}{2} | D. \left|x+\frac{1}{2}\right| > \frac{5}{2} |
| Zadanie 16. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10192 |
Podpunkt 16.1 (1 pkt)
« Wyznacz największą liczbę całkowitą dodatnią spełniającą nierówność
|x+12| \lessdot 23.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 17. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10193 |
Podpunkt 17.1 (1 pkt)
Przedział liczb \langle -a,a\rangle
jest rozwiązaniem nierówności:
Dane
a=18
Odpowiedzi:
| A. |x| > 18 | B. |x| \geqslant 18 |
| C. |x|\leqslant 18 | D. |x| \lessdot 18 |
| Zadanie 18. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10194 |
Podpunkt 18.1 (1 pkt)
Suma przedziałów
(-\infty, a\rangle\cup \langle b,+\infty)
jest zbiorem rozwiązań nierówności:
Dane
a=4
b=8
b=8
Odpowiedzi:
| A. \left|x-6\right| \geqslant 2 | B. \left|x-6\right| > 2 |
| C. \left|x-6\right| \lessdot 2 | D. \left|x-6\right| \leqslant 2 |
| Zadanie 19. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10199 |
Podpunkt 19.1 (1 pkt)
Wskaż liczbę, która spełnia równanie:
\left| \frac{2}{a}x-3 \right| = -\frac{4}{a}x-2
Dane
a=9
Odpowiedzi:
| A. -15 | B. -\frac{45}{2} |
| C. 15 | D. \frac{45}{2} |
| Zadanie 20. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10196 |
Podpunkt 20.1 (1 pkt)
« Wskaż liczbę, która spełnia równanie:
\left| 2ax-2 \right| = -6ax
Dane
a=6
Odpowiedzi:
| A. -\frac{1}{12} | B. -\frac{1}{19} |
| C. -\frac{1}{13} | D. \frac{1}{24} |
| Zadanie 21. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10198 |
Podpunkt 21.1 (1 pkt)
« Wskaż liczbę, która spełnia równanie
\left| 3-x-a \right| = 2x+2a+6:
Dane
a=12
Odpowiedzi:
| A. -9 | B. -7 |
| C. -13 | D. -15 |
| E. -8 | F. -16 |
| Zadanie 22. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10195 |
Podpunkt 22.1 (1 pkt)
Wskaż nierówność, którą spełnia liczba \pi:
Odpowiedzi:
| A. \left| x+\frac{14}{3}\right| \geqslant 8 | B. \left| x \right| \lessdot 3 |
| C. \left| x+7\right| > 11 | D. \left| x+\frac{29}{3}\right|\leqslant 13 |
| Zadanie 23. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10187 |
Podpunkt 23.1 (1 pkt)
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
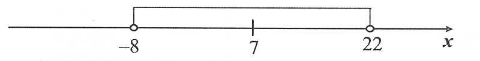
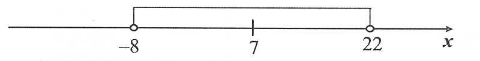
Odpowiedzi:
| A. |x-7| > 15 | B. |x-7| \lessdot 15 |
| C. |x-15| \lessdot 7 | D. |x-15| > 7 |
| Zadanie 24. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11457 |
Podpunkt 24.1 (1 pkt)
Dane są liczby:
x=\frac{3\frac{2}{5}+4,6:2\frac{7}{8}+a}{0,(3)}
oraz
y=2\left|1-\sqrt{2}\right|-\left|2\sqrt{2}-2\right|+|-4|\cdot |2|
.
Liczba x-y jest:
Dane
a=-\frac{2}{3}=-0.666666666667
Odpowiedzi:
| A. całkowita dodatnia | B. niewymierna ujemna |
| C. równa \sqrt{2}-1 | D. całkowita ujemna |
| Zadanie 25. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20866 |
Podpunkt 25.1 (2 pkt)
Ile rozwiązań ma równanie |x|+\sqrt{a}=c-b?
Dane
a=8
b=2
c=4
b=2
c=4
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 25.2 (2 pkt)
Ile rozwiązań ma to równanie dla poniższych danych?
Dane
a=6
b=1.5
c=4
b=1.5
c=4
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)