Twierdzenie Pitagorasa
Zadania dla klasy pierwszej liceum ogólnokształcącego - poziom podstawowy
|
| Zadanie 1. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11463 |
Podpunkt 1.1 (1 pkt)
Dwa boki trójkąta maja długość 18 i
37. Trzeci bok tego trójkąta należy do przedziału
(a,b).
Wyznacz liczby a i b.
Odpowiedzi:
| a | = |
(wpisz liczbę zapisaną dziesiętnie) |
| b | = |
(wpisz liczbę zapisaną dziesiętnie) |
| Zadanie 2. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11462 |
Podpunkt 2.1 (1 pkt)
Trójkąt o bokach długości \sqrt{2}+1,
\sqrt{2}+1, a:
Dane
a=2+\sqrt{2}=3.41421356237310
Odpowiedzi:
| A. jest ostrokątny | B. jest rozwartokątny |
| C. jest prostokątny | D. nie istnieje |
| Zadanie 3. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-10583 |
Podpunkt 3.1 (1 pkt)
Trójkąt równoramienny prostokątny ma przeciwprostokątną długości
a+b\sqrt{2}.
Oblicz pole powierzchni tego trójkąta.
Dane
a=7
b=4
b=4
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. (1 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-11560 |
Podpunkt 4.1 (1 pkt)
Które z podanych trójek są długościami boków trójkąta rozwartokątnego?
Odpowiedzi:
| T/N : 14, 14, 20 | T/N : 2\sqrt{10}, 2\sqrt{6}, 2\sqrt{5} |
| T/N : 8, 10, 12 |
| Zadanie 5. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20712 |
Podpunkt 5.1 (2 pkt)
Punkt O jest środkiem okręgu na rysunku:
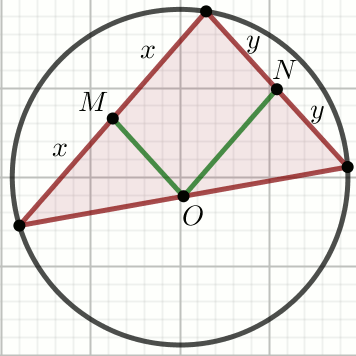

Oblicz długość tego okręgu.
Dane
x=27=27.00000000000000
y=\frac{45}{4}=11.25000000000000
y=\frac{45}{4}=11.25000000000000
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20713 |
Podpunkt 6.1 (1 pkt)
« Długości dwóch najkrótszych boków trójkąta prostokątnego pozostają w stosunku
a:b, a obwód tego trójkąta ma długość
L.
Wyznacz długość najkrótszego boku tego trójkąta.
Dane
L=140
a=20
b=21
a=20
b=21
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.2 (1 pkt)
Wyznacz długość najdłuższego boku tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20714 |
Podpunkt 7.1 (2 pkt)
« Czworokąt na rysunku jest prostokątem. Oceń, czy kąt
\alpha jest prosty, ostry czy rozwarty:
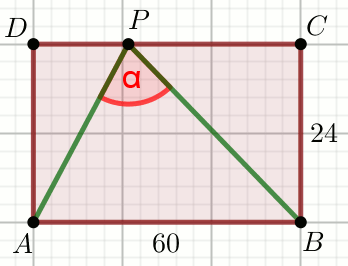

Jeśli kąt \alpha jest prosty wpisz 0, jeśli ostry wpisz 1, jeśli rozwarty wpisz 2.
Dane
|DP|:|PC|=\frac{1}{5}=0.20
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20241 |
Podpunkt 8.1 (2 pkt)
W trójkącie równoramiennym
AC oraz BC są ramionami.
Oblicz pole powierzchni tego trójkąta.
Dane
|AC|=\sqrt{425}=20.61552812808830
|BC|=\sqrt{425}=20.61552812808830
|AB|=40
|BC|=\sqrt{425}=20.61552812808830
|AB|=40
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20243 |
Podpunkt 9.1 (1 pkt)
» Boki trójkąta prostokątnego mają długości: a,
6 i b.
Podaj najmniejszą możliwą wartość a.
Dane
b=14
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 9.2 (1 pkt)
Podaj największą możliwą wartość a.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20875 |
Podpunkt 10.1 (1 pkt)
W trójkącie prostokątnym najkrótszy bok ma długość 10, a
najdłuższy bok jest dłuższy od dłuższej przyprostokątnej o 4.
Oblicz długość dłuższej przyprostokątnej tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 10.2 (1 pkt)
Oblicz obwód tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 11. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pp-20873 |
Podpunkt 11.1 (2 pkt)
Obwód trójkąta prostokątnego ma długość \frac{35}{2}, a
stosunek długość przyprostokątnych tego trójkąta jest równy
20:21.
Oblicz długość przeciwprostokątnej tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)