Twierdzenie sinusów
Zadania dla klasy pierwszej liceum ogólnokształcącego - poziom rozszerzony
|
| Zadanie 1. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20561 |
Podpunkt 1.1 (2 pkt)
« Dany jest trójkąt:
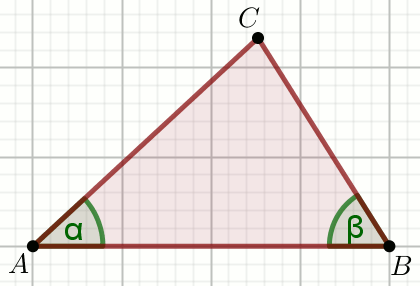

Oblicz |AC|.
Dane
\sin\alpha=\frac{3}{7}=0.42857142857143
\cos\beta=\frac{2}{7}=0.28571428571429
|BC|=8
\cos\beta=\frac{2}{7}=0.28571428571429
|BC|=8
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20563 |
Podpunkt 2.1 (2 pkt)
« Promień okręgu opisanego na trójkącie ABC ma
długość R:
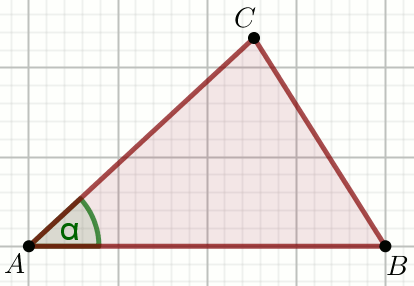

Oblicz sumę sinusów wszystkich kątów tego trójkąta.
Dane
|AB|=48
|AC|=25
\cos\alpha=\frac{24}{25}=0.96000000000000
R=\frac{625}{14}=44.64285714285710
|AC|=25
\cos\alpha=\frac{24}{25}=0.96000000000000
R=\frac{625}{14}=44.64285714285710
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20564 |
Podpunkt 3.1 (2 pkt)
« Dany jest trójkąt:


Oblicz miarę największego kąta tego trójkąta.
Dane
|AB|=4\sqrt{2}=5.65685424949238
|BC|=4=4.00000000000000
|AC|=(1+\sqrt{3})\cdot 2\sqrt{2}=7.72740661031255
\alpha=30^{\circ}
|BC|=4=4.00000000000000
|AC|=(1+\sqrt{3})\cdot 2\sqrt{2}=7.72740661031255
\alpha=30^{\circ}
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20565 |
Podpunkt 4.1 (2 pkt)
« Dany jest trójkąt:
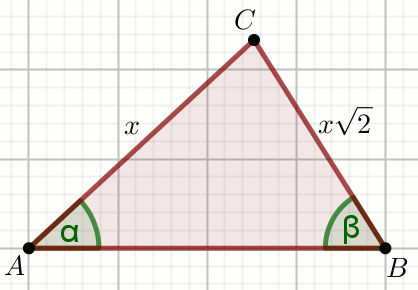

Oblicz \frac{\cos^2\alpha}{2\cos^2\beta-1}.
Dane
x=6
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20738 |
Podpunkt 5.1 (2 pkt)
» W trójkącie ostrokątnym ABC dane są:
długość boku AB oraz tangens kąta przy
wierzchołku C.
Oblicz długość promienia koła opisanego na tym trójkącie.
Dane
\tan\alpha=\frac{40}{9}=4.44444444444444
|AB|=42
|AB|=42
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20770 |
Podpunkt 6.1 (2 pkt)
Dwa boki trójkąta mają długości a i
b. Dowolny punkt boku trzeciego połączono
z wierzchołkiem kąta naprzeciwległego odcinkiem, który podzielił
ten trójkąta na dwa mniejsze trójkąty.
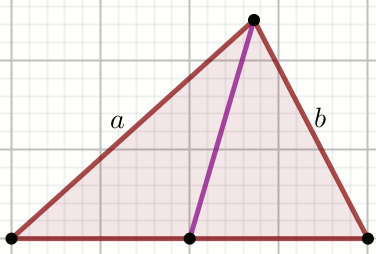

Oblicz stosunek długości promieni okręgów opisanych na otrzymanych trójkątach. Podaj wartość tego stosunku należącą do przedziału \langle 1,+\infty).
Dane
a=3
b=4
b=4
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20769 |
Podpunkt 7.1 (2 pkt)
« Dany jest trójkąt ABC, w którym
|BC|=\frac{6\sqrt{2}}{5},
|\sphericalangle CAB|=45^{\circ},
|\sphericalangle BCA|=30^{\circ}.
Oblicz |AB|.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)