Twierdzenie cosinusów
Zadania dla klasy pierwszej liceum ogólnokształcącego - poziom rozszerzony
|
| Zadanie 1. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20740 |
Podpunkt 1.1 (1 pkt)
« Kąt ostry DAB równoległoboku
ABCD ma miarę \alpha.
Oblicz długość krótszej przekątnej tego równoległoboku.
Dane
\alpha=60^{\circ}
|AB|=3
|AD|=7
|AB|=3
|AD|=7
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 1.2 (1 pkt)
Oblicz długość dłuższej przekątnej tego równoległoboku.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 2. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20741 |
Podpunkt 2.1 (1 pkt)
Dwa boki trójkąta mają długość a i
b, a \alpha jest kątem
zawartym między nimi.
Wyznacz najmniejszą możliwą długość trzeciego boku tego trójkąta.
Dane
a=8
b=4
\sin\alpha=\frac{3\sqrt{7}}{8}=0.99215674164922
b=4
\sin\alpha=\frac{3\sqrt{7}}{8}=0.99215674164922
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 2.2 (1 pkt)
Wyznacz największą możliwą długość trzeciego boku tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 3. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20742 |
Podpunkt 3.1 (2 pkt)
« Dany jest trójkąt ABC. Oblicz miarę kąta
CAB.
Dane
|AB|=\sqrt{2}=1.41421356237310
|BC|=\sqrt{26}=5.09901951359278
|AC|=4\sqrt{2}=5.65685424949238
|BC|=\sqrt{26}=5.09901951359278
|AC|=4\sqrt{2}=5.65685424949238
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 4. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20743 |
Podpunkt 4.1 (2 pkt)
» Oblicz długość niebieskiego odcinka na rysunku:
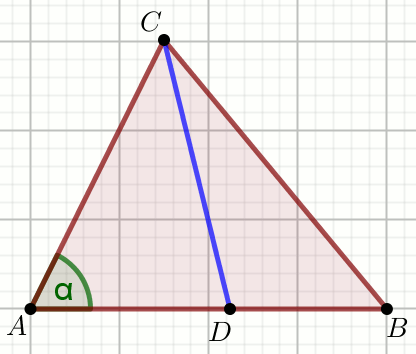

Dane
|AD|=10
|DB|=5
|AC|=26
|BC|=\sqrt{601}=24.51530134426253
|DB|=5
|AC|=26
|BC|=\sqrt{601}=24.51530134426253
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 5. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20744 |
Podpunkt 5.1 (2 pkt)
» Oblicz długość promienia okręgu na rysunku:
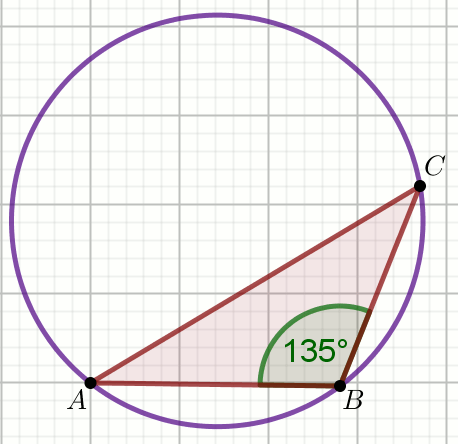

Dane
|AC|-|AB|=18\sqrt{2}=25.45584412271571
|BC|=30
|BC|=30
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 6. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20745 |
Podpunkt 6.1 (1 pkt)
« Dany jest trójkąt ABC:
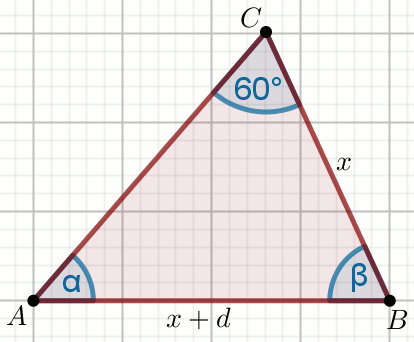

Oblicz \sin\alpha.
Dane
d=6
|AC|=12
|AC|=12
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 6.2 (1 pkt)
Oblicz \sin\beta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 7. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20747 |
Podpunkt 7.1 (2 pkt)
« Trójkąt na rysunku jest równoboczny:
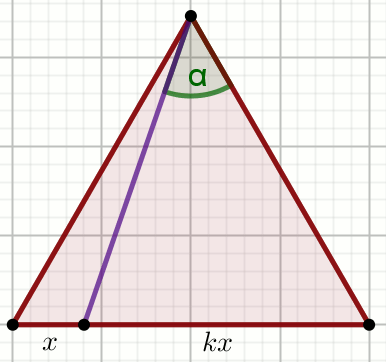

Oblicz \sin\alpha.
Dane
k=3
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 8. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20800 |
Podpunkt 8.1 (2 pkt)
Oblicz długość środkowej trójkąta o bokach długości
a, b i
c, poprowadzonej do najdłuższego boku.
Dane
a=5
b=10
c=13
b=10
c=13
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 9. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20746 |
Podpunkt 9.1 (2 pkt)
» Dany jest trójkąt:
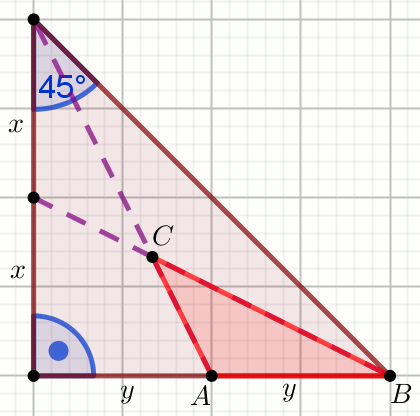

Oblicz \cos\sphericalangle BCA.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 10. (2 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-20442 |
Podpunkt 10.1 (2 pkt)
» Dwa okręgi o środkach O_1 i
O_2 i promieniu 2 są styczne,
jeden zewnętrznie, a drugi wewnętrznie do trzeciego okręgu o środku
O i promieniu 8.
Wiedząc, że |\sphericalangle O_1OO_2|=60^{\circ} oblicz |O_1O_2|.
Odpowiedź:
Wpisz odpowiedź:
(wpisz odpowiedź tekstową)
| Zadanie 11. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30348 |
Podpunkt 11.1 (4 pkt)
» Oblicz obwód trójkąta na rysunku:
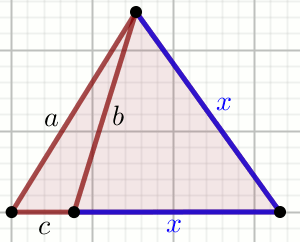

Dane
a=48
b=42
c=18
b=42
c=18
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 12. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30379 |
Podpunkt 12.1 (2 pkt)
«« Pole powierzchni trójkąta o kącie ostrym 30^{\circ} jest
równe 18\sqrt{3}, a promień okręgu na nim opisanego
ma długość 6.
Podaj długość najdłuższego boku tego trójkąta.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 12.2 (1 pkt)
Podaj długość promienia okręgu opisanego na tym trójkącie.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 12.3 (1 pkt)
Podaj długość promienia okręgu wpisanego w ten trójkąt.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 13. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30380 |
Podpunkt 13.1 (4 pkt)
« W trójkącie na rysunku dane są długości odcinków:
|AD|=2,
|DB|=5,
|BC|=4\sqrt{2} i
|AC|=5:
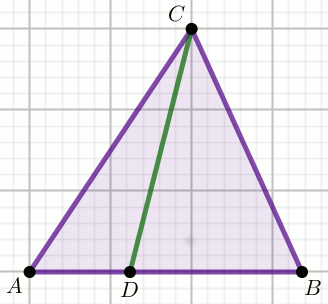

Oblicz \sin\sphericalangle{ADC}.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
| Zadanie 14. (4 pkt) | [ ⇒ Dodaj do testu ] Numer zadania: pr-30794 |
Podpunkt 14.1 (1 pkt)
(2 pkt) W prostokącie ABCD dane są długości boków AB
i AD. Na boku CD zaznaczono punkt
E, zaś na odcinku EB punkt
M (zobacz rysunek).
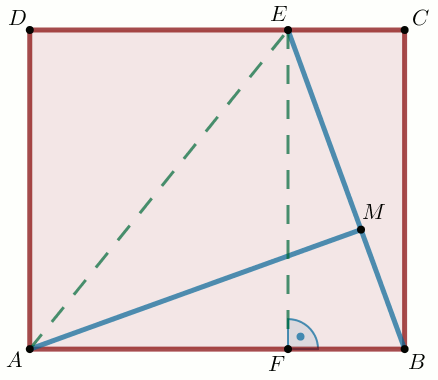

Wykorzystując podane poniżej długości odcinków oblicz pole powierzchni trójkąta ABM.
Dane
|AB|=13
|AD|=12
|DE|=8
|EM|=12
|AD|=12
|DE|=8
|EM|=12
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.2 (1 pkt)
(1 pkt) Oblicz długość odcinka AM.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)
Podpunkt 14.3 (2 pkt)
(1 pkt) Oblicz długość promienia okręgu opisanego na trójkącie
ABM.
Odpowiedź:
Wpisz odpowiedź:
(liczba zapisana dziesiętnie)